Uma equipe internacional de pesquisadores interdisciplinares identificou métricas matemáticas para caracterizar a fragilidade dos mercados financeiros. Seu artigo "Geometria da rede e instabilidade do mercado" lança luz sobre a arquitetura de ordem superior dos sistemas financeiros e permite que os analistas identifiquem riscos sistêmicos como bolhas ou quedas de mercado.

Com a recente corrida de pequenos investidores para os chamados "estoques de meme" e o ressurgimento do interesse em criptomoedas, falar de instabilidade do mercado, volatilidade crescente, e bolhas estourando estão surgindo. Contudo, "As teorias econômicas tradicionais não podem prever eventos como o colapso das hipotecas subprime dos EUA em 2007", de acordo com o autor do estudo, Areejit Samal. Ele e seus colegas de mais de dez matemáticos, física, economia, e instituições focadas em sistemas complexos em todo o mundo deram um grande passo na caracterização da instabilidade do mercado de ações.

O artigo resume a complexidade do mercado financeiro em uma rede de ações e emprega medidas de rede inspiradas na geometria para avaliar a fragilidade do mercado e a dinâmica financeira. Eles analisaram e compararam as redes do mercado de ações para os índices USA S &P500 e japonês Nikkei-225 para um período de 32 anos (1985-2016) e pela primeira vez foram capazes de mostrar que várias curvaturas discretas de Ricci são excelentes indicadores de instabilidades de mercado . O trabalho foi publicado recentemente no Royal Society Open Science jornal e permite que os analistas façam a distinção entre períodos de 'negócios como de costume' e tempos de fragilidade, como bolhas ou quedas de mercado.

A rede criada pela conexão de ações com preços e volumes de negociação altamente correlacionados constitui a base estrutural de seu trabalho. Os pesquisadores então empregam quatro curvaturas discretas, desenvolvido pelo diretor do Instituto Max Planck de Matemática nas Ciências Jürgen Jost e seus colegas de trabalho, para estudar as mudanças na estrutura das redes do mercado de ações ao longo do tempo. Suas comparações com outras métricas de estabilidade de mercado mostraram que suas quatro noções de curvatura servem como indicadores genéricos de instabilidade de mercado.

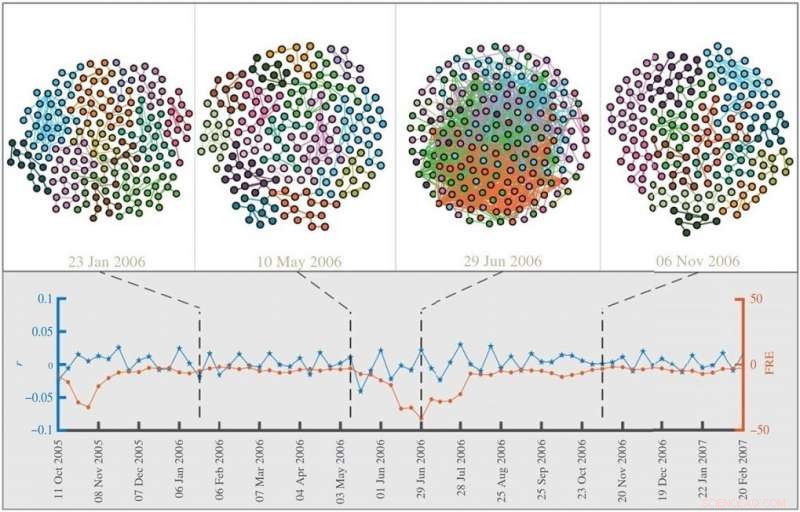
Um candidato a curvatura, a curvatura de Forman-Ricci (FRE), tem uma correlação particularmente alta com indicadores financeiros tradicionais e pode capturar com precisão o medo do mercado (volatilidade) e a fragilidade (risco). Seu estudo confirma que em períodos normais de negociação, o mercado é muito fragmentado, ao passo que, em tempos de bolhas e quedas iminentes do mercado, as correlações entre as ações se tornam mais uniformes e altamente interconectadas. O FRE é sensível às flutuações do mercado global e impulsionadas pelo setor e, enquanto os indicadores comuns, como os retornos, permanecem imperceptíveis, as curvaturas da rede expõem essas dinâmicas e atingem valores extremos durante uma bolha. Assim, o FRE pode capturar as interdependências dentro e entre setores que facilitam a propagação de perturbações e aumentam o perigo de quebra do mercado.

O diretor do Instituto Max Planck de Matemática nas Ciências, Jürgen Jost, resume a dificuldade de analisar a fragilidade do mercado:"não há definições fáceis de um crash ou bolha do mercado e apenas monitorar os índices de mercado estabelecidos ou os retornos logados não é suficiente, mas nossa metodologia oferece uma ferramenta poderosa para examinar continuamente o risco de mercado e, portanto, a saúde do sistema financeiro. "Os insights obtidos por este estudo podem ajudar os tomadores de decisão a compreender melhor o risco sistêmico e identificar os pontos de inflexão, que pode potencialmente prever crises financeiras vindouras ou possivelmente até evitá-los completamente.