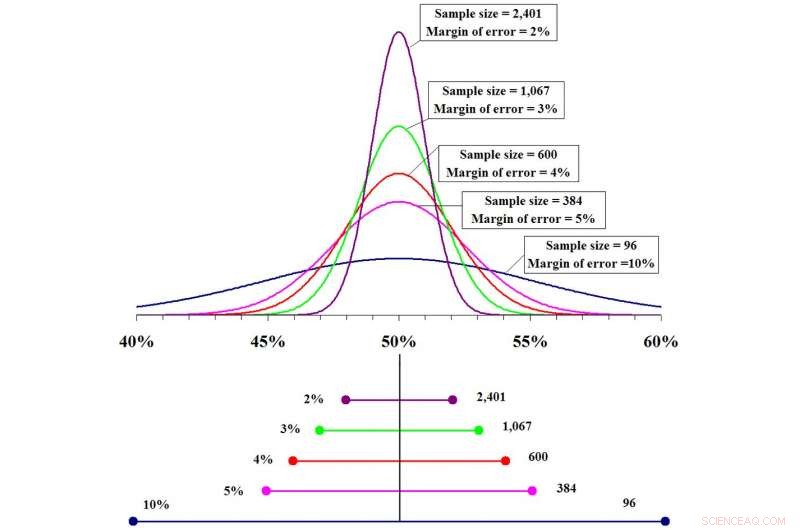
Quanto maior o tamanho da amostra, quanto mais precisa a previsão e menor a margem de erro. Crédito:Fadethree via Wikimedia Commons
No ano passado, as estatísticas têm sido extraordinariamente importantes nas notícias. Qual é a precisão do teste COVID-19 que você ou outras pessoas estão usando? Como os pesquisadores sabem a eficácia de novas terapêuticas para pacientes COVID-19? Como as redes de televisão podem prever os resultados das eleições muito antes de todas as cédulas terem sido contadas?
Cada uma dessas questões envolve alguma incerteza, mas ainda é possível fazer previsões precisas, desde que essa incerteza seja compreendida. Uma ferramenta que os estatísticos usam para quantificar a incerteza é chamada de margem de erro.
Dados limitados
Eu sou um estatístico, e parte do meu trabalho é fazer inferências e previsões. Com tempo e dinheiro ilimitados, Eu poderia simplesmente testar ou pesquisar todo o grupo de pessoas em que estou interessado para avaliar a pergunta em mente e encontrar a resposta exata. Por exemplo, para descobrir a taxa de infecção de COVID-19 nos EUA, Eu poderia simplesmente testar toda a população dos EUA. Contudo, no mundo real, você nunca pode acessar 100% de uma população.
Em vez de, os estatísticos amostram uma pequena porção da população e constroem um modelo para fazer uma previsão. Usando a teoria estatística, esse resultado da amostra é extrapolado para representar toda a população.
Idealmente, uma boa amostra deve ser representativa da população total, incluindo gênero, diversidade racial, diversidade socioeconômica, padrões de estilo de vida e outras medidas demográficas. Quanto maior a amostra, mais semelhante seria com a população real, e com uma amostra maior, os estatísticos mais confiantes se tornam em suas previsões. Mas sempre haverá alguma incerteza.
Quantificação da incerteza
Veja o desenvolvimento de drogas, por exemplo. É sempre verdade prever que um novo medicamento terá algo entre 0% e 100% de eficácia para todos na Terra. Mas essa não é uma previsão muito útil. O trabalho de um estatístico é restringir esse intervalo a algo mais útil. Os estatísticos costumam chamar esse intervalo de intervalo de confiança, e é a faixa de previsões dentro da qual os estatísticos estão muito confiantes de que o número verdadeiro será encontrado.
Se um medicamento foi testado em 10 indivíduos e sete deles acharam eficaz, a eficácia estimada do medicamento é de 70%. Mas, uma vez que o objetivo é prever a eficácia em toda a população, os estatísticos precisam levar em conta a incerteza de testar apenas 10 pessoas.
Os intervalos de confiança são calculados usando uma fórmula matemática que abrange o tamanho da amostra, a gama de respostas e as leis de probabilidade. Neste exemplo, o intervalo de confiança seria entre 42% e 98% - um intervalo de 56 pontos percentuais. Depois de testar apenas 10 pessoas, você poderia dizer com grande confiança que o medicamento é eficaz para entre 42% e 98% das pessoas em toda a população.
Se você dividir o intervalo de confiança pela metade, você obtém a margem de erro - neste caso, 28%. Quanto maior a margem de erro, menos precisa a previsão. Quanto menor for a margem de erro, mais precisa será a previsão. Uma margem de erro de quase 30% ainda é um intervalo bastante amplo.
Contudo, imagine que os pesquisadores testaram esta nova droga em 1, 000 pessoas em vez de 10 e foi eficaz em 700 delas. A eficácia estimada do medicamento ainda será em torno de 70%, no entanto, essa previsão é muito mais precisa. O intervalo de confiança para a amostra maior ficará entre 67% e 73%, com margem de erro de 3%. Você poderia dizer que se espera que esta droga seja 70% eficaz, mais ou menos 3%, para toda a população.
Os estatísticos adorariam prever com 100% de precisão o sucesso ou o fracasso de um novo medicamento ou os resultados exatos de uma eleição. Contudo, isso não é possível. Sempre há alguma incerteza, e a margem de erro é o que quantifica essa incerteza; deve ser considerado ao observar os resultados. Em particular, a margem de erro define o intervalo de previsões dentro do qual os estatísticos estão muito confiantes de que o número verdadeiro será encontrado. Uma margem de erro aceitável é uma questão de julgamento com base no grau de precisão exigido nas conclusões a serem tiradas.
Este artigo foi republicado de The Conversation sob uma licença Creative Commons. Leia o artigo original. 