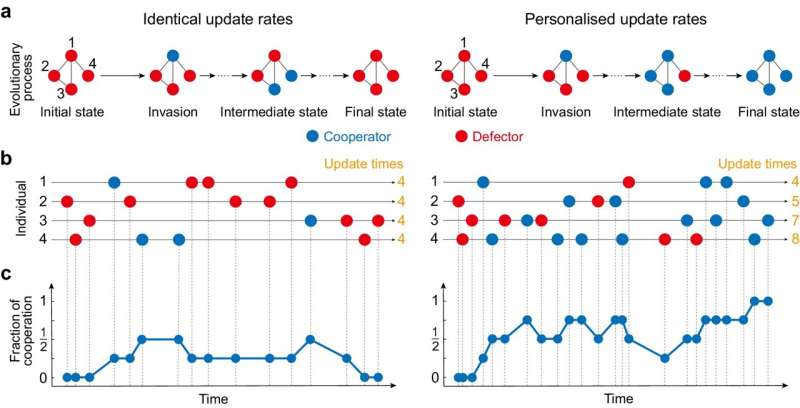
 Ilustração do processo evolutivo com taxas de atualização de estratégia idênticas versus personalizadas. Crédito:Nature Communications (2024). DOI:10.1038/s41467-024-47380-8
Ilustração do processo evolutivo com taxas de atualização de estratégia idênticas versus personalizadas. Crédito:Nature Communications (2024). DOI:10.1038/s41467-024-47380-8 Qual é a melhor maneira de um grupo de indivíduos cooperar? Esta é uma questão de longa data com raízes na teoria dos jogos, um ramo da ciência que utiliza modelos matemáticos de como os indivíduos devem traçar a melhor estratégia para obter o resultado ideal.
Um exemplo simples é o dilema do prisioneiro:duas pessoas são presas por um suposto assalto a banco. A polícia os leva para o centro da cidade e os coloca em salas de interrogatório individuais e isoladas.
A polícia admite não ter provas suficientes para condenar os dois e dá a mesma opção a cada um:se ele confessar e o companheiro não, libertarão o confessor e condenarão o outro pela grave acusação de assalto a banco. Mas se um não confessar e o outro o fizer, o primeiro receberá uma longa pena de prisão e o outro será libertado. Se ambos confessarem, ambos serão presos por muitos anos. Se nenhum deles confessar, serão acusados por uma acusação menor de porte de arma.
O que cada um deve fazer para minimizar o tempo na prisão? Um indivíduo fica em silêncio, confiando que seu parceiro fará o mesmo e aceitará uma pena de prisão mais curta? Ou ele confessa, esperando que o outro fique em silêncio. Mas e se o outro também confessar? É uma posição nada invejável.
Não existe uma solução correta para o dilema do prisioneiro. Outros problemas semelhantes são o jogo da galinha, onde cada piloto corre em direção ao outro, arriscando uma colisão frontal ou desviando no último minuto e arriscando a humilhação – sendo chamado de “galinha” por falta de coragem. Existem muitos outros jogos simples.
Agora imagine um grupo - eles podem ser pessoas ou algum tipo de organismo celular. Que tipo de cooperação proporciona o resultado ideal, quando cada indivíduo está ligado a outros e paga um custo (dinheiro, energia, tempo) para criar um resultado que beneficie a todos? É um facto que os indivíduos são egoístas e agem no seu melhor interesse, mas também sabemos que a cooperação pode resultar num resultado melhor para todos. Alguém correrá o risco ou cuidará apenas de si mesmo?
Um resultado de longa data é que, numa rede homogénea onde todos os indivíduos têm o mesmo número de vizinhos, a cooperação é favorecida se a relação entre o benefício proporcionado por um cooperador e o custo associado pago excede o número médio de vizinhos.
 Uma expressão analítica do algoritmo OptUpRat que produz a estratégia de cooperação ideal para um grupo de nós em uma rede. Crédito:Aming Li, por meio de uma licença Creative Commons Attribution 4.0 International
Uma expressão analítica do algoritmo OptUpRat que produz a estratégia de cooperação ideal para um grupo de nós em uma rede. Crédito:Aming Li, por meio de uma licença Creative Commons Attribution 4.0 International
Mas as pessoas não são homogéneas, são heterogéneas e normalmente não têm o mesmo número de ligações aos vizinhos que todas as outras pessoas, nem mudam a sua estratégia ao mesmo ritmo.
Sabe-se também que permitir que cada indivíduo atualize a sua estratégia exatamente ao mesmo tempo, como imitar imediatamente o seu vizinho, altera significativamente a evolução da cooperação. Investigações anteriores relataram que conexões individuais heterogêneas e generalizadas dificultam a cooperação quando se presume que os indivíduos atualizam suas estratégias em taxas idênticas.
Agora, um grupo de investigadores localizados na China, no Canadá e nos EUA encontrou um resultado surpreendente:quando as taxas de actualização da estratégia dos indivíduos variam inversamente com o seu número de ligações, as ligações heterogéneas superam as homogéneas na promoção da cooperação. O estudo foi publicado na revista Nature Communications .
"Como analisar o impacto quantitativo das estruturas de rede heterogêneas predominantes no surgimento de estratégias ótimas de grupo é uma questão aberta de longa data que tem atraído muita atenção", disse Aming Li, coautor e professor assistente de Dinâmica e Controle na Universidade de Pequim.
A equipe de Li resolveu o problema por meio de cálculos analíticos apoiados por simulações computacionais, para encontrar a regra fundamental para manter a cooperação coletiva:“Os nós com conexões substanciais dentro do sistema complexo devem atualizar suas estratégias com pouca frequência”, diz ele. Ou seja, as taxas de atualização de estratégias individuais devem variar inversamente com o número de conexões que possuem na rede. Desta forma, uma rede com ligações heterogéneas entre indivíduos supera uma rede com ligações homogéneas na promoção da cooperação.
A equipe também desenvolveu um algoritmo que encontra com mais eficiência as taxas ideais de atualização de estratégia que geram as estratégias ideais do grupo, que eles chamam de OptUpRat. Este algoritmo ajuda na utilidade coletiva em grupos e, diz Li, “também é essencial no desenvolvimento de sistemas colaborativos robóticos”. A descoberta será útil para pesquisadores em áreas multidisciplinares como cibernética, inteligência artificial, ciência de sistemas, teoria dos jogos e ciência de redes.
“Acreditamos que a utilização de técnicas relacionadas à IA para otimizar decisões individuais e impulsionar a inteligência coletiva será o próximo ponto de pesquisa”.

