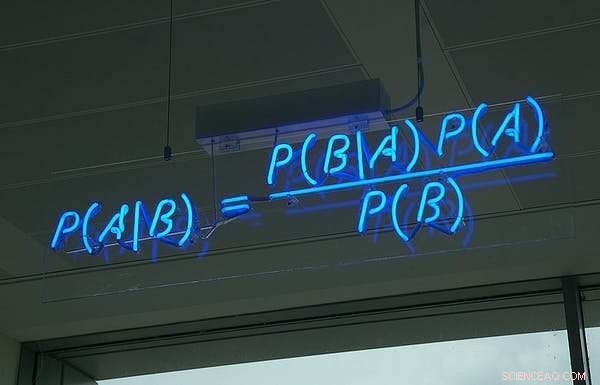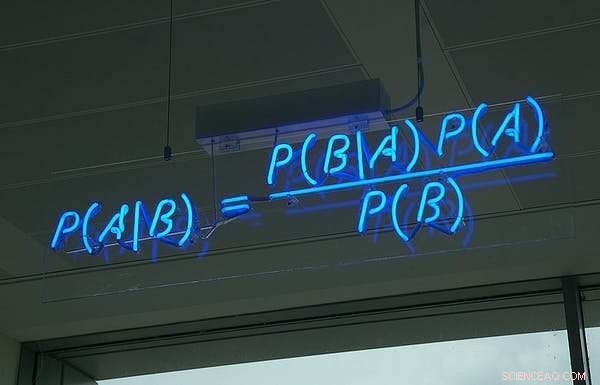
Teorema de Bayes, em neon, no escritório da empresa britânica de software HP Autonony. Crédito:Wikimedia Commons, CC BY
As catastróficas inundações da costa leste da Austrália foram descritas pelo primeiro-ministro de NSW como um "evento de 1.000 anos, um termo que criou muita confusão.
Longas explicações de que esses termos não são o mesmo que "ocorrendo com 1.000 anos de diferença" ou "uma vez a cada 1.000 anos" só aumentaram a confusão.
A explicação mais simples é que o significado real de "um em 1.000 anos" é "ter uma probabilidade de 0,1% em qualquer ano" (1 em 1.000), o que levanta a questão:por que as pessoas simplesmente não dizem isso?
A principal razão é que esses termos remontam a uma época em que a maioria das pessoas não pensava em termos de probabilidades, e mesmo aqueles que pensavam estavam confusos sobre como funcionavam. Hoje em dia interagimos com probabilidades o tempo todo.
A previsão meteorológica diária inclui uma probabilidade percentual de chuva, e as previsões de longo prazo dão as probabilidades de chuvas acima ou abaixo da média de acordo com os ciclos El Niño e La Niña.
Os mercados financeiros apostam nas probabilidades ou nos movimentos das taxas de juro. Estatística e probabilidade são ensinadas às crianças na escola.
Mas este é um desenvolvimento bastante recente.
Até o século XVII, mesmo os conceitos mais elementares da teoria das probabilidades eram desconhecidos. As pessoas pensavam em destino e fortuna como essencialmente incognoscíveis. Mesmo os jogadores não entendiam as probabilidades.
O nascimento da probabilidade De fato, foi um pedido de um amigo jogador por volta de 1654 que motivou o filósofo e matemático francês Blaise Pascal a desenvolver os conceitos básicos de probabilidade com o colega matemático Pierre de Fermat.
(Pascal também usou a ideia para desenvolver a "aposta de Pascal" usada para demonstrar a utilidade de acreditar em Deus. A ideia é que, se Deus existe, os crentes serão recompensados com a bem-aventurança eterna. Se não, eles renunciarão a um número limitado de prazeres terrenos enquanto Não importa quão pequena seja a probabilidade de Deus existir, o benefício de acreditar em Deus acaba sendo infinito enquanto o custo é finito.)
A compreensão se desenvolveu lentamente. Não foi até meados do século 18 que o clérigo inglês Thomas Bayes foi creditado com o desenvolvimento mais importante do campo.
A ferramenta legada por Bayes Em sua interpretação moderna, o teorema de Bayes nos dá os meios para revisar nossa visão da probabilidade de um evento à luz das evidências sobre o que acabou de acontecer.
Se algo acabou de acontecer ou não, é explicitamente inserido no recálculo junto com avaliações atualizadas da probabilidade de que isso seja importante.
Até Bayes, a maioria das probabilidades eram calculadas como se fossem imutáveis, como a probabilidade de obter "cara" ao jogar uma moeda. Essas probabilidades poderiam ser descritas de maneira útil como "uma em 1.000 anos" ou "em média, a cada segundo lance".
Mas a probabilidade de uma inundação severa muda ao longo do tempo à medida que a relação entre os componentes que compõem o sistema climático muda. Se uma inundação ocorreu nos dá evidências sobre essa mudança.
Isso faz com que não seja mais útil se referir a uma inundação severa como um evento "um em x anos".
Já passou muito da época em que mudamos a terminologia de uma vez em tantos anos, mas para quê? A resposta parece simples, embora os detalhes sejam complicados.
Primeiro, precisamos converter as medidas antigas em escalas de gravidade, semelhantes às usadas para ciclones e terremotos, mas específicas para cada bacia.
Feito isso, a probabilidade de um evento de determinada gravidade pode ser estimada com base na experiência histórica e atualizada à luz de novas evidências.
Como isso se aplicaria no caso de um evento como a inundação de Lismore?
A descrição inicial de "um em 1.000 anos" significa que tal evento seria extremamente improvável se o antigo relacionamento se mantivesse.
Usando o teorema de Bayes, atualizaríamos a probabilidade inicial em 1.000 com base em informações atualizadas sobre a chance de as relações subjacentes estarem mudando, produzindo novas probabilidades anuais a cada ano.
É assim que o aprendizado de máquina funciona e como as probabilidades médicas e de seguro são atualizadas. Infelizmente, as probabilidades revisadas quase certamente excederão uma em 1.000.