Fórmula matemática pioneira abre caminho para avanços empolgantes na saúde, energia e indústria alimentícia
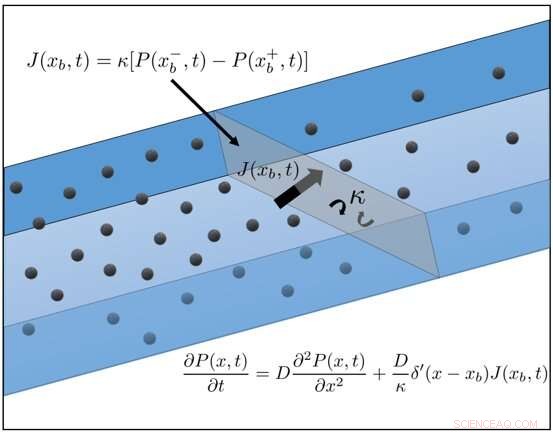
Uma nova equação inovadora foi desenvolvida para modelar o movimento difusivo através de material permeável exatamente pela primeira vez. Crédito:Universidade de Bristol
Uma equação matemática inovadora que poderia transformar procedimentos médicos, extração de gás natural e produção de embalagens plásticas no futuro foi descoberta.
A nova equação, desenvolvida por cientistas da Universidade de Bristol, indica que o movimento difusivo através de material permeável pode ser modelado exatamente pela primeira vez. Ele vem um século depois que os físicos líderes mundiais Albert Einstein e Marian von Smoluchowski derivaram a primeira equação de difusão e marca um importante progresso na representação do movimento para uma ampla gama de entidades, desde partículas microscópicas e organismos naturais até dispositivos feitos pelo homem.
Até agora, os cientistas que observavam o movimento das partículas através de materiais porosos, como tecidos biológicos, polímeros, várias rochas e esponjas, dependiam de aproximações ou perspectivas incompletas.
As descobertas, publicadas hoje na revista
Physical Review Research , fornecem uma nova técnica que apresenta oportunidades interessantes em uma ampla gama de configurações, incluindo saúde, energia e indústria de alimentos.
O autor principal Toby Kay, que está concluindo um Ph.D. em Engenharia Matemática, disse:"Isso marca um passo fundamental desde os estudos de Einstein e Smoluchowski sobre difusão. Ele revoluciona a modelagem de entidades difusoras através de meios complexos de todas as escalas, de componentes celulares e compostos geológicos a habitats ambientais.
"Anteriormente, as tentativas matemáticas de representar o movimento através de ambientes repletos de objetos que impedem o movimento, conhecidas como barreiras permeáveis, eram limitadas. animais, organismos celulares e humanos."
A criatividade na matemática assume diferentes formas e uma delas é a conexão entre diferentes níveis de descrição de um fenômeno. Nesse caso, ao representar o movimento aleatório de forma microscópica e, em seguida, diminuir o zoom para descrever o processo macroscopicamente, foi possível encontrar a nova equação.
Mais pesquisas são necessárias para aplicar esta ferramenta matemática em aplicações experimentais, que podem melhorar produtos e serviços. Por exemplo, ser capaz de modelar com precisão a difusão de moléculas de água através do tecido biológico avançará na interpretação das leituras de MRI (Imagem por Ressonância Magnética) ponderadas por difusão. Também poderia oferecer uma representação mais precisa do ar se espalhando pelos materiais de embalagem de alimentos, ajudando a determinar o prazo de validade e o risco de contaminação. Além disso, quantificar o comportamento de animais forrageiros interagindo com barreiras macroscópicas, como cercas e estradas, poderia fornecer melhores previsões sobre as consequências das mudanças climáticas para fins de conservação.
O uso de geolocalizadores, telefones celulares e outros sensores viu a revolução do rastreamento gerar dados de movimento de quantidade e qualidade cada vez maiores nos últimos 20 anos. Isso destacou a necessidade de ferramentas de modelagem mais sofisticadas para representar o movimento de entidades amplas em seu ambiente, de organismos naturais a dispositivos feitos pelo homem.
O autor sênior Dr. Luca Giuggioli, Professor Associado em Ciências da Complexidade da Universidade de Bristol, disse:"Esta nova equação fundamental é outro exemplo da importância de construir ferramentas e técnicas para representar a difusão quando o espaço é heterogêneo; isto é, quando o ambiente muda de local para local.
"Ele se baseia em outra resolução há muito esperada em 2020 de um enigma matemático para descrever o movimento aleatório em espaço confinado. movimento - que tem muitas aplicações potenciais interessantes."
+ Explorar mais Solução para problema matemático centenário pode prever transmissão de doenças infecciosas
