
Exemplo de uma seção transversal da superfície K3 no espaço 3, semelhante a um modelo da Utah State University e da University of Missouri-St. Os matemáticos de Louis costumavam examinar as dualidades das cordas entre a teoria F e a teoria heterótica em oito dimensões. Crédito:USU
Simplificando, a teoria das cordas é um método proposto para explicar tudo. Na realidade, não há nada de simples nisso. A teoria das cordas é uma estrutura teórica da física que descreve unidimensional, vibrando objetos fibrosos chamados "cordas, "que se propagam pelo espaço e interagem entre si. Peça por peça, mentes energéticas estão descobrindo e decifrando cordas fundamentais do universo físico usando modelos matemáticos. Entre esses intrépidos exploradores estão os matemáticos da Universidade do Estado de Utah, Thomas Hill, e seu mentor, Andreas Malmendier.
Com o colega Adrian Clingher, da University of Missouri-St. Louis, a equipe publicou descobertas sobre dois ramos da teoria das cordas no jornal, "A dualidade entre a teoria F e a corda heterótica em D =8 com duas linhas de Wilson, "em 7 de agosto, Edição online de 2020 de Letters in Mathematical Physics. O trabalho dos pesquisadores da USU é apoiado por uma bolsa da Fundação Simons.
"Estudamos uma família especial de superfícies K3 - compactas, superfícies complexas conectadas de dimensão 2 - que são ferramentas geométricas importantes para a compreensão de simetrias de teorias físicas, "diz Hill, que se formou no Programa de Honras da USU com bacharelado em matemática em 2018 e concluiu um mestrado em matemática na primavera passada. "Nesse caso, estávamos examinando a dualidade das cordas entre a teoria F e a teoria heterótica das cordas em oito dimensões. "
Hill diz que a equipe provou que as superfícies K3 investigadas admitem quatro maneiras exclusivas de fatiar as superfícies como fibras elípticas Jacobianas, formações de fibras em forma de toro. Os pesquisadores construíram equações explícitas para cada uma dessas fibrações.
"Uma parte importante desta pesquisa envolve a identificação de certos blocos de construção geométrica, chamados de 'divisores, "dentro de cada superfície K3, "ele diz." Usando esses divisores, informações geométricas cruciais são então codificadas em um gráfico abstrato. "
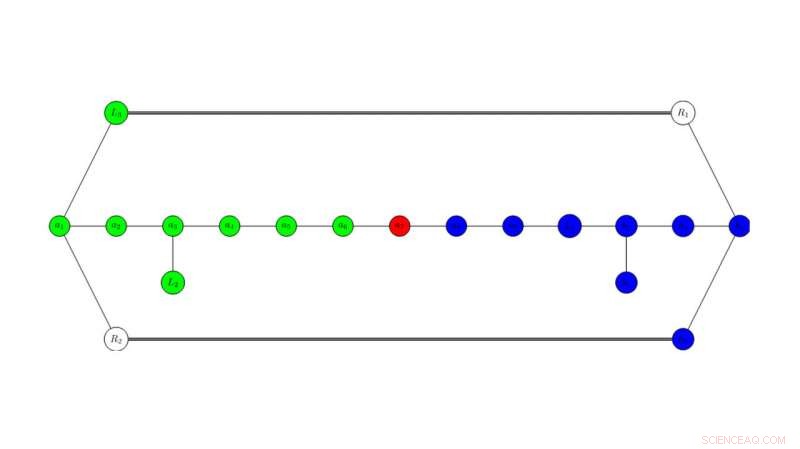
Usando um gráfico abstrato, Pesquisadores da Universidade do Estado de Utah identificam divisores dentro de cada superfície K3 para examinar simetrias variadas. As diferentes fibrações elípticas Jacobianas correspondem a cores específicas de um subconjunto conectado dos nós do gráfico. As simetrias do gráfico e as possíveis cores dos nós são cruciais para a compreensão das simetrias das teorias físicas subjacentes. Crédito:Malmendier / Hill, USU
Este processo, Hill diz, permite que os pesquisadores investiguem simetrias de teorias físicas subjacentes demonstradas pelo gráfico.
"Você pode pensar nesta família de superfícies como um pão e cada fibra como uma 'fatia' desse pão, "diz Malmendier, professor associado do Departamento de Matemática e Estatística da USU. "Ao examinar a sequência de fatias, podemos visualizar, e entender melhor, o pão inteiro. "
O empreendimento descrito no artigo, ele diz, representa horas de trabalho árduo de "papel e lápis" para provar teoremas de cada uma das quatro fibrações, seguido por empurrar cada teorema através de fórmulas algébricas difíceis.
"Para a última parte deste processo, usamos o software Maple e o pacote especializado de geometria diferencial desenvolvido na USU, que simplificou nossos esforços computacionais, "Malmendier diz.