 p As cadeias de montanhas da Terra compartilham as mesmas características universais. Eles se tornam visíveis quando o mapa topográfico (aqui:os Alpes da Ligúria) é transformado em um mapa de cristas. (Fonte:IFJ PAN) Crédito:Fonte:IFJ PAN
p As cadeias de montanhas da Terra compartilham as mesmas características universais. Eles se tornam visíveis quando o mapa topográfico (aqui:os Alpes da Ligúria) é transformado em um mapa de cristas. (Fonte:IFJ PAN) Crédito:Fonte:IFJ PAN
p As montanhas têm caráter. O gentil contínuo, colinas onduladas e amplos vales dos Cárpatos, Apalaches ou partes inferiores dos Alpes contrastam fortemente com os picos elevados, cristas irregulares e ravinas profundas das altas montanhas Tatra e Pirineus, que são, por sua vez, diferente do inacessível, gigantes cobertos de neve do Himalaia ou dos Andes, ao longo de cujas encostas fluem longas línguas de geleiras em vez de água. Por baixo desta grande diversidade, Contudo, encontra-se uma estrutura surpreendentemente semelhante. p Usando gráficos e fractais, cientistas do Instituto de Física Nuclear da Academia Polonesa de Ciências (IFJ PAN) em Cracóvia observaram a estrutura dos maciços do nosso planeta. Variações tão diversas como os Alpes, os Pirenéus, as montanhas escandinavas, as montanhas Baetic, o Himalaia, os Andes, os Apalaches, as Montanhas Atlas e os Alpes do Sul foram todos submetidos à lupa estatística. A análise, apresentado no
Journal of Complex Networks , resultou em uma observação inesperada. Acontece que existe uma semelhança universal na estrutura dos maciços terrestres. Pode ser visto em cadeias de montanhas em todos os continentes, independentemente do tamanho dos picos, a idade deles, ou mesmo se são de origem tectônica ou vulcânica.
p "Parece que a única coisa que as várias cadeias de montanhas têm em comum é que, quando você olha para elas, você tem que realmente inclinar a cabeça para trás. A semelhança real só se torna visível quando transformamos um mapa topográfico simples das montanhas em um mapa de cordilheira, ou seja, aquele que mostra os eixos de todas as cristas, "diz o Dr. Jaroslaw Kwapien (IFJ PAN), e então acrescenta:"O eixo do cume é uma linha que corre ao longo do topo do cume da montanha de tal forma que em ambos os lados o terreno cai para baixo. Portanto, é o oposto do eixo de um vale."
p Os cumes das montanhas não são criações discretas. Eles se fundem em um grande, estrutura ramificada, semelhante a uma árvore:da crista principal ("o tronco") existem cristas laterais mais longas ou mais curtas de primeira ordem ("ramos"), deles surgem cristas laterais de segunda ordem, e destes subsequentes repetidamente. O conjunto tem uma estrutura claramente hierárquica e o número de graus de complexidade depende do tamanho da área coberta por montanhas e pode chegar a várias dezenas. Estruturas deste tipo são apresentadas na forma de vários gráficos. Por exemplo, cada cume de um determinado maciço pode ser tratado como um nó. Dois nós são conectados por linhas (arestas do gráfico) quando as cristas correspondentes também estão conectadas. Neste tipo de gráfico, alguns nós estão conectados a muitos nós, enquanto outros estão conectados a apenas alguns.
p Os gráficos construídos para diferentes maciços têm diferentes estruturas (topologia). Uma forma de estudá-los é a distribuição do grau do nó, contendo informações sobre o número de nós de um determinado grau. Em distribuições típicas, grandes valores aparecem em nós de baixo grau, porque são os mais numerosos. Normalmente não há muitos nós de alto grau - hubs. No caso das montanhas, o hub principal, geralmente correspondendo ao cume mais longo da cadeia montanhosa estudada, tem um grau de vários milhares. Hubs de segunda ordem, ou seja, cristas laterais da crista principal, tem graus de várias centenas. Os mais numerosos são nós com grau um. Pode haver até várias centenas de milhares deles.
p "A distribuição do grau de nó das cristas acaba por ser de natureza de lei de potência. Isso significa que o número de nós de um certo grau e, por exemplo, o número de nós com um grau que é a metade está em uma relação constante, independentemente do grau selecionado. Cada fragmento da distribuição aumentado por um certo fator constante parece um todo, o que significa que nenhuma escala é distinguida, "diz o Dr. Kwapien.
p Distribuições de lei de potência são encontradas em gráficos que representam sistemas que ocorrem na natureza (por exemplo, ao estudar as ligações entre proteínas e enzimas em uma célula viva), bem como em nossas próprias atividades (como citações de artigos científicos, a cooperação de atores em filmes, a vizinhança das palavras nos textos, links entre sites). Eles costumam se descrever como semelhantes, estruturas fractais. Um dos exemplos de modelo de fractais naturais são montanhas. Seus modelos de computador são gerados até mesmo por algoritmos usando geometria fractal, portanto, a topologia power-law dos gráficos de cristas não deve surpreender ninguém. Contudo, o valor do expoente de potência acabou sendo uma surpresa.
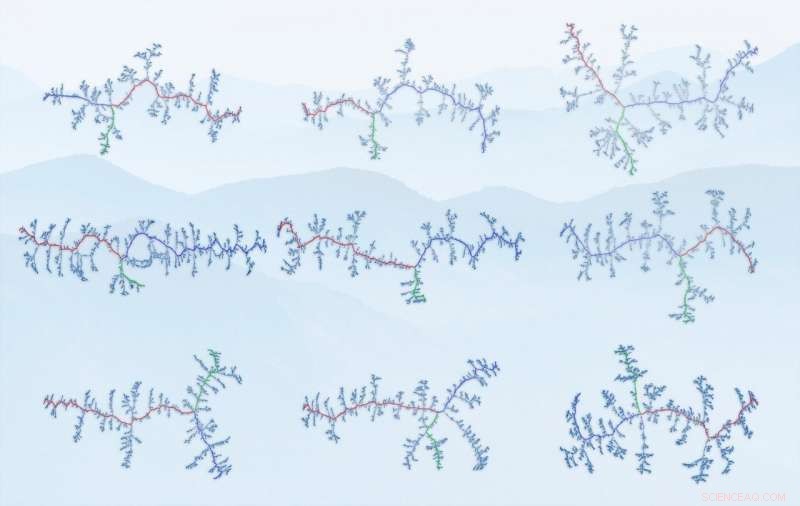 p Gráficos de cume das cadeias de montanhas estudadas. Os nós aqui são as interseções de cristas, as bordas - as próprias cristas. Do canto superior esquerdo:Alpes, Montanhas Baéticas, Pirineus, Montanhas Escandinavas, Himalaia (parte), Alpes do Sul, Montanhas Apalaches, Andes (parte), Montanhas Atlas. (Fonte:IFJ PAN) Crédito:Fonte:IFJ PAN
p Gráficos de cume das cadeias de montanhas estudadas. Os nós aqui são as interseções de cristas, as bordas - as próprias cristas. Do canto superior esquerdo:Alpes, Montanhas Baéticas, Pirineus, Montanhas Escandinavas, Himalaia (parte), Alpes do Sul, Montanhas Apalaches, Andes (parte), Montanhas Atlas. (Fonte:IFJ PAN) Crédito:Fonte:IFJ PAN
p "Independentemente do tipo de montanhas, o expoente da distribuição da lei de potência assumiu valores em uma faixa muito estreita em torno do número 5/3. Se levarmos em consideração a precisão de nossa metodologia, esta estreita faixa de valores pode até significar que os expoentes em cada caso examinado eram os mesmos, "observa o Dr. Kwapien.
p A homogeneidade observada resulta do fato de que em todas as partes do nosso planeta os principais mecanismos responsáveis pela escultura de montanha são basicamente os mesmos. Movimentos tectônicos ou vulcânicos são necessários para elevar o terreno, mas o fator de modelagem mais importante é a erosão hídrica e glacial. Água e gelo levam à rachadura e esmagamento de rochas e transferem o material fragmentado para as terras baixas. Isso resulta em ravinas, desfiladeiros e vales de montanha, e, portanto, também cumes. Como os cursos d'água que formam o sistema de drenagem de uma determinada área são de estrutura dendrítica por natureza (fora das áreas desérticas, claro), uma estrutura semelhante também ocorre no caso dos sistemas de cristas. Mas por que as relações mútuas entre o número de cristas com um número diferente de ramos são tão semelhantes para diferentes tipos de montanhas?
p “A situação fica mais clara quando consideramos a gravidade além da água, "explica o Dr. Kwapien." Quando o material rochoso é triturado, torna-se sujeito à dinâmica de corpos soltos, independentemente de sua composição química. Corpos soltos em encostas só podem permanecer lá se os ângulos de inclinação não forem muito grandes. As encostas não devem ser muito íngremes. É por isso que a profundidade dos vales na natureza é limitada por sua própria largura. Canyons estreitos de rios com paredes quase verticais existem apenas no estágio inicial da formação da escultura. Eles são raros em formações montanhosas maduras porque suas paredes já sofreram inclinação. "
p A existência de sistemas fluviais drenando água de uma determinada área, erosão esmagando rochas e esculpindo vales, bem como deslizamentos gravitacionais de entulho de rocha significam que as cristas não podem estar arbitrariamente próximas ou distantes umas das outras. Existe um arranjo ideal, independente das propriedades da cordilheira e dando às montanhas algumas características universais.
p As observações acima são complementadas por outra observação feita pelos físicos do PAN IFJ, no que diz respeito às dimensões das estruturas da crista fractal. A dimensão fractal descreve o quão áspera é a estrutura do objeto. A linha de uma única crista tem uma dimensão de 1. Se as linhas (cristas) foram colocadas extremamente densamente, sua dimensão fractal corresponderia à dimensão da superfície, e, portanto, seria igual a 2. Os pesquisadores mostraram que se as estruturas de cristas forem apresentadas como grafos cujos nós são as interseções das cristas (é nessas interseções que os picos são mais comuns), e as bordas dos gráficos são as cristas conectando os picos, então as dimensões fractais de tais gráficos seriam com uma boa aproximação igual ao número ... 5/3.
p "Em alguns gráficos, vemos a hierarquia das estruturas montanhosas, em outros, sua fractalidade. Em ambos os casos, para todos os tipos de montanhas encontramos os mesmos valores dos números apropriados. Este universalismo dá o que pensar, "afirma o Prof. Stanislaw Drozdz (IFJ PAN, Universidade de Tecnologia de Cracóvia).
p Se diferentes cadeias de montanhas são tão semelhantes em termos de tamanho, onde estão as fontes da diversidade da montanha? Será possível estudá-los usando a teoria dos grafos e a geometria fractal? Será possível criar um modelo em que um grafo em evolução imite as etapas sucessivas da formação de uma escultura de montanha? Finalmente, será possível aplicar na prática a transformação de mapas de cristas em grafos, por exemplo em cartografia? Essas perguntas - e muitas outras - só serão respondidas por pesquisas futuras.

