Como qualquer um que já teve que escovar cabelos compridos sabe, os nós são um pesadelo. Mas com experiência suficiente, a maioria aprende os truques de desembaraçar com o mínimo de dor – comece na parte inferior, trabalhe até o couro cabeludo com escovas curtas e suaves e aplique o desembaraçador quando necessário.
L. Mahadevan, professor de Matemática Aplicada, de Biologia Organísmica e Evolutiva e de Física da Lola England de Valpine, aprendeu a mecânica de pentear anos atrás enquanto escovava o cabelo de sua filha.

"Lembro que o spray desembaraçante parecia funcionar às vezes, mas eu ainda tinha que ter o cuidado de pentear suavemente, começando pelas pontas livres", disse Mahadevan. "Mas logo fui demitido do emprego porque não era muito paciente."

Embora Mahadevan tenha perdido seu papel como cabeleireiro, ele ainda era um cientista e a topologia, geometria e mecânica do desembaraçar apresentavam questões matemáticas interessantes que são relevantes para uma série de aplicações, incluindo fabricação de têxteis e processos químicos, como processamento de polímeros.

Em um novo artigo, publicado na revista Soft Matter, Mahadevan e os coautores Thomas Plumb Reyes e Nicholas Charles exploram a matemática do pentear e explicam por que a técnica de escovação usada por tantos é o método mais eficaz para desembaraçar um feixe de fibras.

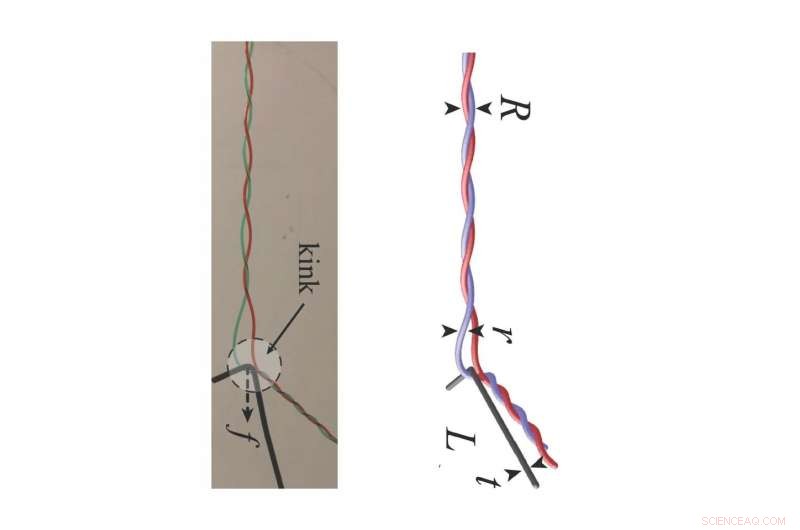
Para simplificar o problema, os pesquisadores simularam dois filamentos entrelaçados helicoidalmente, em vez de uma cabeça inteira de cabelo.

"Usando este modelo mínimo, estudamos o desembaraçar da dupla hélice por meio de um único dente rígido que se move ao longo dela, deixando dois filamentos desembaraçados em seu rastro", disse Plumb-Reyes, estudante de pós-graduação da SEAS. "Medimos as forças e deformações associadas ao pentear e depois simulamos numericamente."

"Traços curtos que começam na extremidade livre e se movem em direção à extremidade presa removem os emaranhados criando um fluxo de uma quantidade matemática chamada 'densidade do elo' que caracteriza a quantidade que os fios de cabelo trançados entre si, consistentes com simulações do processo", disse Nicholas Charles, estudante de pós-graduação da SEAS.

Os pesquisadores também identificaram o comprimento mínimo ideal para cada golpe – qualquer menor e levaria uma eternidade para pentear todos os emaranhados e mais tempo e seria muito doloroso.

Os princípios matemáticos de escovação desenvolvidos por Plumb-Reyes, Charles e Mahadevan foram usados ​​recentemente pela professora Daniela Rus e sua equipe no MIT para projetar algoritmos para escovar o cabelo por um robô.

Em seguida, a equipe pretende estudar a mecânica de escovar os cabelos crespos e como ela responde à umidade e à temperatura, o que pode levar a uma compreensão matemática de um fato que toda pessoa com cabelos crespos conhece:nunca escove os cabelos secos.