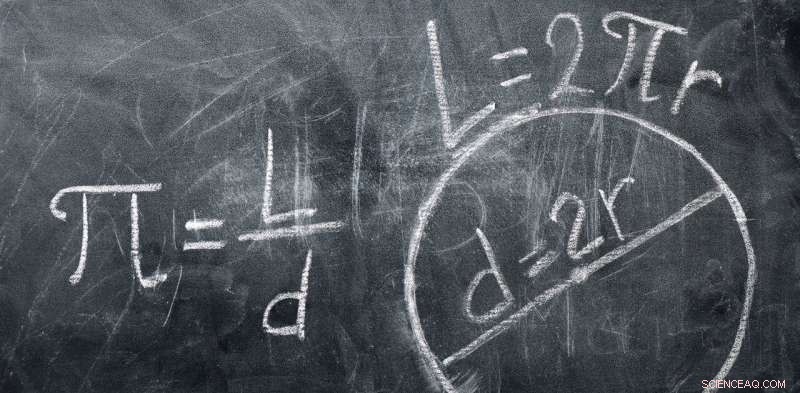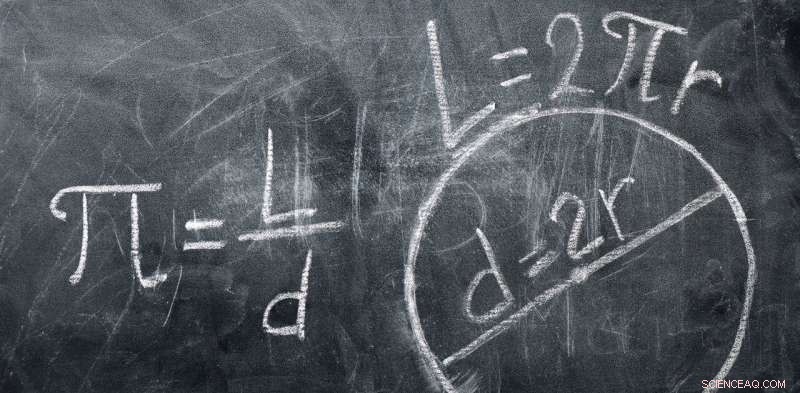 p O que significa para os alunos se eles estão aprendendo que a tecnologia pode responder a todos os desafios?
p O que significa para os alunos se eles estão aprendendo que a tecnologia pode responder a todos os desafios?
p Os computadores ajudaram a pesquisa matemática a acelerar em várias direções e aumentaram a presença da matemática na vida cotidiana. p O papel da tecnologia no ensino e aprendizagem da matemática está cada vez mais em minha mente como um instrutor de matemática que vê novos alunos chegarem à Simon Fraser University (SFU) todos os anos. Ambos na SFU, e quando visito salas de aula de matemática canadenses como palestrante convidado, Eu olho para as salas cheias de jovens vibrantes cercados por calculadoras, computadores e telefones inteligentes.
p E tudo bem. Como muitos matemáticos, Não recuei contra os novos ventos tecnológicos introduzidos pelos tempos modernos. Mas essa tecnologia deve melhorar e estender, ao invés de substituir, a capacidade de pensar matematicamente.
p
Adieu geometria?
p Recentemente, Encontrei-me com um jovem interessado em matemática e computação, mas não tenho certeza de que direção ele gostaria de seguir. Apresentei o seguinte problema usado pela Universidade de Oxford para entrevistar candidatos de graduação em matemática:"Imagine uma escada encostada em uma parede vertical com os pés no chão. O degrau do meio do escada foi pintada com uma cor diferente na lateral, para que possamos ver quando olhamos para a escada de lado. Que forma esse degrau do meio traça quando a escada cai no chão? "
p Uma maneira de abordar o quebra-cabeça da escada é usar, de uma forma relativamente simples, Geometria euclidiana, para mostrar que a resposta é um quarto de círculo. Veja abaixo:
p Em vez de desenhar em propriedades geométricas, o jovem usou a linguagem de programação Python para animar o problema e encontrar a forma necessária. Ele havia aprendido Python sozinho no início daquele verão. Quando eu perguntei a ele sobre triângulos congruentes, o jovem parecia perplexo.
p Situações como esta me fazem temer que, se não for usado com o devido cuidado nas salas de aula, a tecnologia pode privar os alunos de desenvolver totalmente suas habilidades matemáticas e espaciais.
p
Problemas inacessíveis
p O que os matemáticos chamam de "abordagem assistida computacionalmente" permitiu aos pesquisadores explorar e resolver problemas matemáticos que de outra forma seriam inacessíveis. A prova assistida por computador do célebre Teorema das Quatro Cores vem à mente.
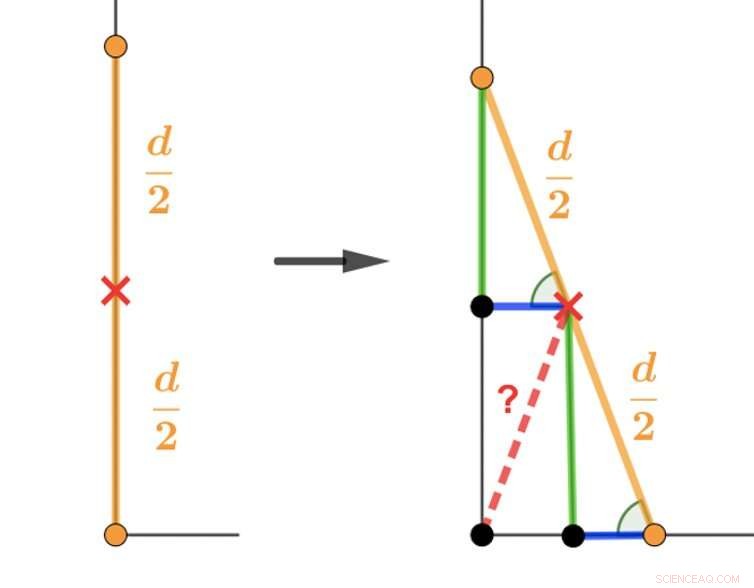 p A geometria euclidiana pode ser usada para resolver o problema apresentado aos candidatos de graduação em matemática da Universidade de Oxford. Crédito:Veselin, Autor fornecido
p A geometria euclidiana pode ser usada para resolver o problema apresentado aos candidatos de graduação em matemática da Universidade de Oxford. Crédito:Veselin, Autor fornecido
p Mas algumas questões matemáticas demonstraram limitações da tecnologia existente - e o fato de que algumas soluções dependem em grande parte da intuição humana, inspiração e inteligência. Um desses problemas, conhecido como o problema da festa (sim, como em um jantar), é encontrar a quantidade de convidados que garantiria que se encontrassem sempre seis pessoas que são amigas em comum ou seis pessoas que são estranhas em comum.
p Em termos matemáticos, este problema é sobre encontrar o que é chamado de "o número Ramsey R (6, 6), "relacionado a um ramo da matemática que estuda quais condições devem existir para que um determinado padrão apareça.
p Acredite ou não, desde 1930 os matemáticos sabem que R (6, 6) existe; desde 1994, sabemos que esse número está entre 102 e 165.
p Nenhum progresso desde então!
p
Matemática experimental
p Os célebres matemáticos canadenses e irmãos Peter Borwein e Jonathan Borwein - que fundaram o Centro de Matemática Experimental e Construtiva em 1993 na SFU - estavam entre os pioneiros da pesquisa que contribuíram para o processo de alinhamento da matemática com as novas tecnologias.
p Conforme sugerido por Jonathan Borwein e o matemático David H. Bailey, a matemática experimental usa "uma abordagem assistida por computador para a pesquisa matemática." Eles queriam dizer que a matemática experimental é sobre o uso de computadores para impulsionar processos que têm sido os elementos básicos da pesquisa matemática por séculos:
- Obtendo percepção e intuição
- Visualizando princípios matemáticos
- Descobrindo novos relacionamentos
- Testando e, especialmente, falsificando conjecturas
- Explorar um resultado possível para tomar uma decisão baseada em evidências, se o resultado possível merecer prova formal
- Sugestão de abordagens para prova formal
p Eles também argumentaram que os computadores poderiam ajudar na realização de derivações matemáticas extensas e na confirmação de resultados derivados analiticamente.
p O que eles queriam dizer era que os computadores permitem que os pesquisadores levem suas explorações a dimensões novas ou diferentes.
O teorema das quatro cores. p
Nova exploração
p As ideias de Bailey e Borwein podem ser usadas para ajudar a descrever formas contemporâneas e futuras de ensino de matemática para ajudar os alunos a olhar para os problemas de novas maneiras.
p Na minha anedota de geometria Python, Eu poderia ter desafiado o aluno observando que a forma obtida pela animação gerada por Python parece apenas um quarto de círculo (isso pode se referir aos pontos 1-3 e 5 na definição de Bailey-Borwein) e que uma resposta completa exigiria um resultado obtido analiticamente (ponto 6).
p Para justificar o desafio, Eu também posso escolher mostrar ao aluno uma prova visual aparentemente alucinante, como a animação que "mostra" 64 =65.
p Posso concluir citando o matemático e filósofo do século 17 René Descartes, que resolveu:"... nunca aceitar nada como verdadeiro que eu não soubesse claramente ser tal; isto é, com cuidado ... evite ... preconceito, e não incluir nada mais em meu julgamento do que o que foi apresentado à minha mente de forma tão clara e distinta a ponto de excluir todo fundamento de dúvida. "
p
Currículos de matemática experimental
p Pesquisadores e educadores desenvolveram currículos especializados em ensinar crianças e jovens a usar computadores para aprimorar e estender seu próprio aprendizado matemático e pensamento em escolas de ensino médio canadenses. Por exemplo, O Projeto de Currículo RabbitMath, liderado pelo matemático Peter Taylor da Queen's University e Chris Suurtamm da University of Ottawa, ou o Projeto Callysto, patrocinado pelo Pacific Institute for Mathematical Sciences (PIMS) e pela organização sem fins lucrativos Cybera, sediada em Alberta.
p O desafio para a comunidade de ensino de matemática será cada vez mais criar e manter um equilíbrio saudável em nossas salas de aula entre o poder do rigor, matemática formal e o poder da computação.
p Quando penso no futuro, Estou preocupado que as partes rigorosas e formais da matemática possam desaparecer e ficar fora do escopo dos alunos.
p Para um estudante em um futuro não muito distante, seria, por exemplo, o número pi se torna um número racional - ou seja, seria igual à sua aproximação gerada pelo computador mais poderoso do momento?
p Mais importante, o que tudo isso significará para os alunos e sua aprendizagem da matemática como um instrumento para navegar melhor pelo mundo ao seu redor? p Este artigo foi republicado de The Conversation sob uma licença Creative Commons. Leia o artigo original.