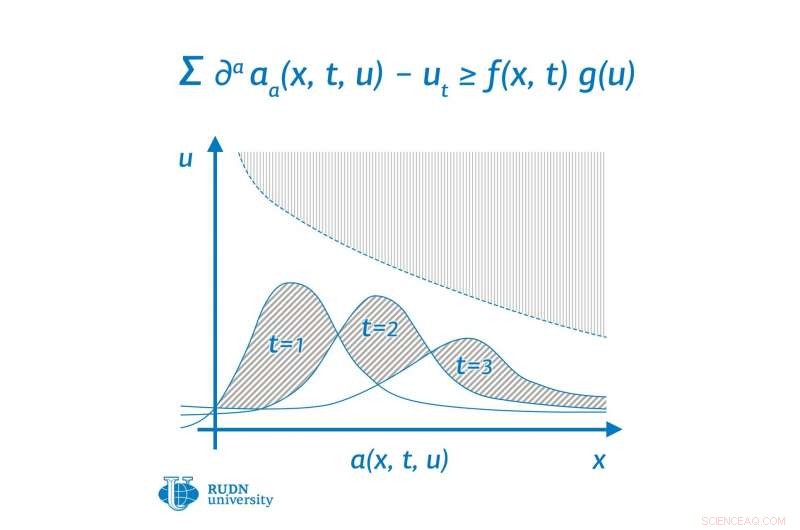
p Um matemático da Universidade RUDN (Rússia) e um colega determinaram as condições para a estabilização das desigualdades diferenciais de alta ordem. Este resultado permitirá aos matemáticos obter restrições nas soluções de equações que descrevem alguns processos físicos, como processos de difusão e processos de convecção. O artigo é publicado na revista Análise Assintótica . p O interesse nas desigualdades diferenciais surge de um grande número de problemas de modelagem matemática nas ciências naturais, bem como na resolução de problemas técnicos e físicos. Freqüentemente, é necessário definir várias funções relacionadas a várias desigualdades diferenciais. É necessário ter o mesmo número de desigualdades para fazer isso. Se cada uma dessas desigualdades for diferencial, isso é, tem a forma de uma relação conectando funções desconhecidas e seus derivados, este é um sistema de desigualdades diferenciais. Os sistemas de desigualdades diferenciais descrevem processos físicos reais com um certo grau de precisão (por exemplo, dispositivos que registram fenômenos físicos não são perfeitos e apresentam alguns erros). Pode ser que um pequeno erro nos dados iniciais cause mudanças significativas na solução da desigualdade. Portanto, é importante definir limites para as soluções de equações diferenciais.

p Andrey Shishkov de S.M. Nikol'skii Mathematical Institute da RUDN University e Andrej Kon'kov da Moscow State University obtiveram o resultado, que generaliza a condição clássica de Keller-Osserman para equações diferenciais. O teorema de Keller-Osserman contém condições para a ausência de soluções positivas para desigualdades elípticas não lineares de segunda ordem. Este teorema serve de base para estudos da ausência de soluções para equações e desigualdades. Além disso, para operadores diferenciais de alta ordem, todos os estudos previamente conhecidos foram limitados ao caso de não linearidade de potência. O caso de não linearidade arbitrária foi estudado apenas para operadores de segunda ordem. Os matemáticos pesquisaram desigualdades diferenciais de ordens superiores e seu resultado se aplica a uma ampla classe de problemas - equações de segunda e terceira ordem.

p Os resultados podem ser aplicados a desigualdades parabólicas e às chamadas desigualdades antiparabólicas. Equações parabólicas são muito difundidas na física:incluem equações que descrevem os processos de convecção, difusão e seu caso particular - a equação de condução de calor; o sistema de equações de Navier-Stokes que descreve o movimento de líquidos e gases é um sistema de equações parabólicas com restrições divergentes.

p As questões foram estudadas anteriormente principalmente para operadores diferenciais de segunda ordem, e o caso de operadores de ordem superior é muito menos estudado. Os matemáticos pesquisaram desigualdades diferenciais de ordem superior e obtiveram condições de estabilização suficientes para as chamadas soluções fracas de desigualdades diferenciais. Ao mesmo tempo, as condições iniciais não são estipuladas nas soluções da desigualdade diferencial estudada. Os autores também não estipulam condições de elipticidade nos coeficientes do operador diferencial.