
Quantos lagos existem no Alasca? Os lagos Thermokarst na encosta norte do Alasca são semelhantes e fractais. Crédito:Pintura de Cherissa Dukelow, CC BY-SA
Respirar. Conforme seus pulmões se expandem, o ar preenche 500 milhões de alvéolos minúsculos, cada um com uma fração de milímetro de diâmetro. Conforme você expira, esses milhões de minúsculas respirações se fundem sem esforço por meio de vias aéreas cada vez maiores em uma respiração final.
Essas vias aéreas são fractais.
Fractais são uma ferramenta matemática para descrever objetos com detalhes em todas as escalas. Matemáticos e físicos como eu usam fractais e conceitos relacionados para entender como as coisas mudam do pequeno ao grande.
Você e eu traduzimos escalas muito diferentes quando pensamos sobre como nossas escolhas afetam o mundo. Este café com leite está contribuindo para a mudança climática? Devo votar nesta eleição?
Essas ferramentas conceituais se aplicam ao corpo e também às paisagens, desastres naturais e sociedade.
Fractais em todos os lugares
Em 1967, o matemático Benoit Mandelbrot perguntou, "Qual é a extensão da costa da Grã-Bretanha?"
É uma pergunta capciosa. A resposta depende de como você o mede. Se você traçar o contorno em um mapa, você recebe uma resposta, mas se você caminhar pela costa com uma régua, o resultado é bem diferente. Qualquer pessoa que tenha tentado estimar a extensão de uma trilha acidentada a partir de um mapa conhece a traição da imagem em grande escala.
Isso é porque os pulmões, a costa britânica e as trilhas para caminhadas têm fractalidade:seu comprimento, o número de ramos ou alguma outra quantidade depende da escala ou resolução que você usa para medi-los.
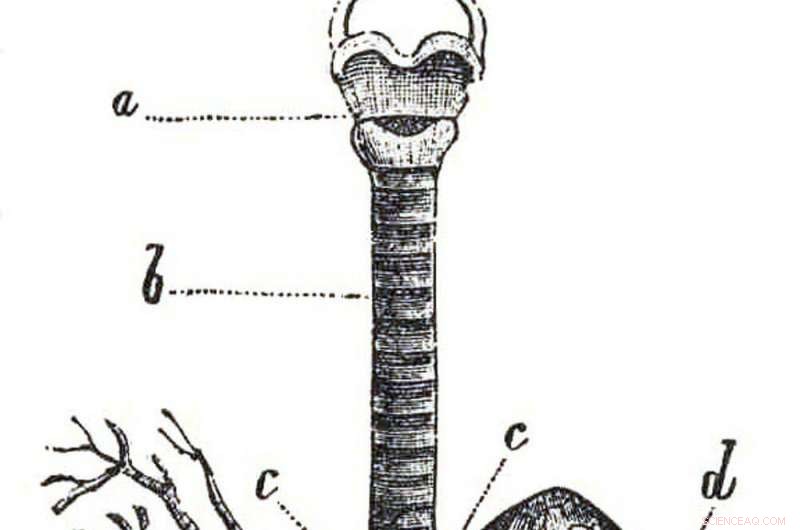
As ramificações dentro dos pulmões são um exemplo de autossimilaridade. Crédito:Dicionário Enciclopédico de Brockhaus e Efron / Wikimedia
O litoral também é auto-semelhante - é feito de cópias menores de si mesmo. Folhas de samambaia, árvores, conchas de caracol, paisagens, as silhuetas de montanhas e redes de rios parecem versões menores de si mesmas.
É por isso, quando você está olhando para uma fotografia aérea de uma paisagem, muitas vezes é difícil dizer se a barra de escala deve ser de 50 km ou 500 m.
Seus pulmões são semelhantes, porque o corpo calibra com precisão cada ramo em proporções exatas, tornando cada ramo uma réplica menor do anterior. Este design modular torna os pulmões eficientes em qualquer tamanho. Pense em uma criança e um adulto, ou um mouse, uma baleia. A única diferença entre pequenos e grandes está em quantas vezes as vias aéreas se ramificam.
Auto-similaridade e fractalidade aparecem na arte e na arquitetura, nos arcos dentro dos arcos dos aquedutos romanos e nas torres das catedrais góticas que refletem a copa da floresta. Até os antigos calígrafos chineses Huai Su e Yan Zhenqing valorizavam a fractalidade das nuvens de verão, rachaduras em uma parede e manchas de água em uma casa com vazamentos em 722.
Invariância de escala
Objetos auto-semelhantes têm uma invariância de escala. Em outras palavras, alguma propriedade é mantida, independentemente de quão grande seja, como a eficiência dos pulmões.
Com efeito, a invariância de escala descreve o que muda entre as escalas, dizendo o que não muda.

Imagem de satélite da Grã-Bretanha e da Irlanda do Norte. Crédito:NASA
Leonardo da Vinci observou que, como galhos de árvores, a área transversal total de todos os ramos é preservada. Em outras palavras, indo do tronco para os galhos, o número de ramos e sua mudança de diâmetro com cada ramificação, mas a espessura total de todos os ramos agrupados permanece a mesma.
A observação de Da Vinci implica uma invariância de escala:para cada ramo de um determinado raio, existem quatro ramos a jusante com metade desse raio.
A frequência de terremotos tem uma invariância de escala semelhante, que foi observada na década de 1940. Os grandes vêm à mente - Lisboa 1755, São Francisco, 1989 - mas muitos pequenos terremotos ocorrem na Califórnia todos os dias. A lei de Gutenberg-Richter diz que a frequência dos terremotos depende do tamanho do terremoto. A resposta é surpreendentemente simples. Um terremoto dez vezes maior ocorre com aproximadamente um décimo da freqüência.
Sociedade e a lei de potência
Um economista do século 19 Vilifredo Pareto - famoso na escola de negócios pela regra 80/20 - observou que o número de famílias com certa riqueza é inversamente proporcional à sua riqueza, elevado a algum expoente. Pareto mediu o expoente para diferentes anos e diferentes países e descobriu que costumava ficar em torno de 1,5.
A distribuição da riqueza de Pareto passou a ser conhecida como a lei do poder, ostensivamente por causa do expoente ou "poder".
Qualquer coisa semelhante a si mesma tem uma lei de potência correspondente. Em um jornal de abril, meu colega e eu descrevemos a lei de potência correspondente para os pulmões, vasos sanguíneos e árvores. Ela difere da lei de potência de Pareto apenas por levar em consideração relações específicas entre ramos.
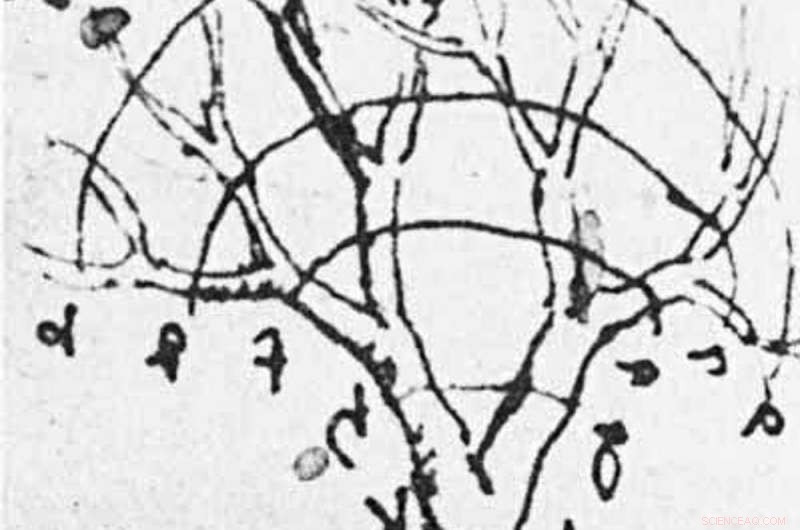
Um esboço das notas de Leonardo da Vinci sobre galhos de árvores. Crédito:Fractal Foundation
Os tamanhos das fortunas, então, são semelhantes aos tamanhos dos galhos das árvores ou vasos sanguíneos - alguns troncos ou galhos grandes e galhos exponencialmente mais minúsculos.
Pareto pensava em sua distribuição de riqueza como uma lei natural, mas muitos modelos diferentes de organização social dão origem a uma distribuição de Pareto e as sociedades variam em desigualdade de riqueza. O expoente de Pareto superior, quanto mais igualitária a sociedade.
Desde a compreensão de como os humanos são compostos de células minúsculas até como afetamos o planeta, auto-similaridade, A fractalidade e a invariância de escala muitas vezes ajudam a traduzir de um nível de organização para outro.
Este artigo foi republicado de The Conversation sob uma licença Creative Commons. Leia o artigo original. 