 p Tarski provou que um círculo com raio de um não pode ser completamente coberto por faixas cuja largura combinada seja menor que dois - o diâmetro do círculo. Cada uma das faixas da imagem tem seu próprio comprimento e cor. Crédito:MIPT
p Tarski provou que um círculo com raio de um não pode ser completamente coberto por faixas cuja largura combinada seja menor que dois - o diâmetro do círculo. Cada uma das faixas da imagem tem seu próprio comprimento e cor. Crédito:MIPT
p O Instituto de Tecnologia de Israel e Alexandr Polyanskii do Instituto de Física e Tecnologia de Moscou (MIPT) provaram a conjectura da zona de László Fejes Tóth. Formulado em 1973, diz que se uma esfera unitária é completamente coberta por várias zonas, sua largura combinada é de pelo menos π. A prova, publicado no jornal
Análise Geométrica e Funcional , é importante para a geometria discreta e permite aos matemáticos formular novos problemas. p A geometria discreta estuda as propriedades combinatórias dos pontos, linhas, círculos, polígonos e outros objetos geométricos. Qual é o maior número de bolas do mesmo tamanho que cabem em volta de outra bola do mesmo tamanho? Qual é a maneira mais densa de compactar círculos de tamanhos iguais em um avião, ou bolas em um espaço de contenção? Essas e outras questões são tratadas pela geometria discreta.
p Soluções para problemas como esses têm aplicações práticas. Assim, o problema de empacotamento denso ajudou a otimizar a codificação e corrigir erros na transmissão de dados. Outro exemplo é o teorema das quatro cores, que diz que quatro cores são suficientes para traçar qualquer mapa em uma esfera de modo que duas regiões adjacentes não tenham a mesma cor. Isso levou os matemáticos a introduzir conceitos importantes para a teoria dos grafos, que é crucial para muitos dos desenvolvimentos recentes na química, biologia e ciência da computação, bem como sistemas de logística.
p A conjectura da zona de Tóth está intimamente relacionada a uma série de outros problemas em geometria discreta que foram resolvidos no século 20, lidando com a cobertura de uma superfície com tiras. O primeiro deles foi o chamado problema da prancha, que envolvia cobrir um disco com tiras delimitadas por linhas paralelas. Alfred Tarski e Henryk Moese ofereceram uma prova simples, mostrando que a largura combinada dessas tiras, ou pranchas, não pode exceder o diâmetro do disco. Isso é, não há melhor maneira de cobrir um disco do que com uma única prancha cuja largura seja igual ao diâmetro do disco. Thøger Bang resolveu então o problema de cobrir um corpo convexo arbitrário com tiras. Nomeadamente, ele provou que a largura combinada das tiras que cobrem um corpo convexo é pelo menos a largura do próprio corpo, isso é, a largura mínima de uma única faixa cobrindo o corpo.
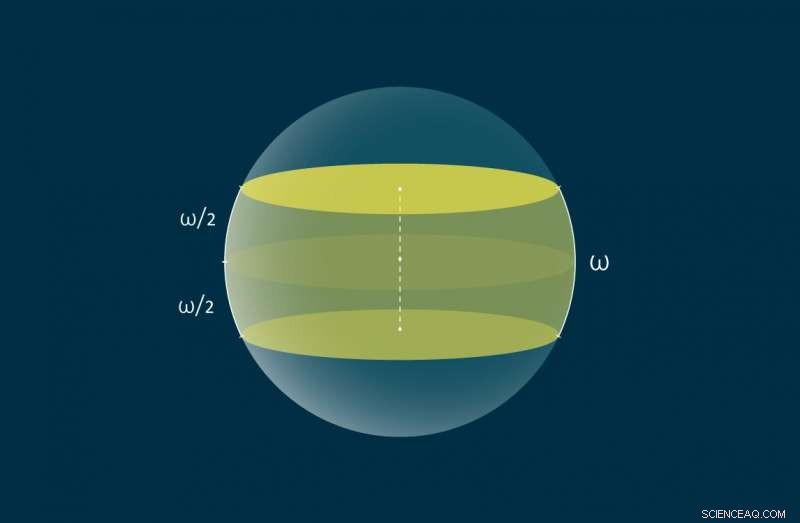 p Uma zona de largura ω na esfera é mostrada em amarelo. Crédito:MIPT
p Uma zona de largura ω na esfera é mostrada em amarelo. Crédito:MIPT
p O problema abordado pelos autores é diferente, pois envolve a cobertura de uma esfera unitária com zonas especialmente construídas. Especificamente, cada zona é a interseção da esfera com uma certa prancha tridimensional, onde uma prancha é a região do espaço contida entre dois planos paralelos que são simétricos em relação ao centro da esfera. Alternativamente, as zonas podem ser definidas no espaço métrico geodésico sem recurso a pranchas:Uma zona de largura ω na superfície de uma esfera unitária é o conjunto de pontos que não se encontram a mais de ω / 2 do grande círculo, ou equador, com as distâncias entre os pontos medidos como os arcos mais curtos conectando-os. Os matemáticos tiveram que encontrar a largura mínima combinada de tais zonas cobrindo a esfera unitária. Assim, o problema difere daqueles resolvidos anteriormente em como a largura é medida - é definida como o comprimento de um arco, em vez da distância euclidiana entre linhas ou planos paralelos.
p A prova apresentada por Jiang e Polyanskii foi inspirada em Bang, que resolveu o problema de cobrir um corpo com tiras, formando um conjunto finito especial de pontos dentro do corpo, um dos quais supostamente não estava coberto por nenhuma das tiras. De certa forma, tanto Bang quanto os autores apresentam uma prova por contradição. No caso da conjectura de Fejes Tóth, os matemáticos levantaram a hipótese de que a largura combinada das zonas que cobriam completamente a esfera era menor que π e procuraram chegar a uma contradição, ou seja, encontre um ponto na esfera, mas não em nenhuma das zonas.
p Os autores mostraram que é possível formar um conjunto de pontos no espaço tridimensional de forma que pelo menos um ponto não seja coberto pelas pranchas que constituem as zonas. Se todo este conjunto estiver dentro da esfera, é então relativamente fácil traçar outro ponto na esfera que também não é coberto pelas pranchas, e, portanto, pelas zonas. Se algum dos pontos do conjunto estiver fora da esfera, acabou sendo possível substituir uma zona maior por várias outras menores, cuja largura combinada é igual à da zona maior. Assim, é possível reduzir o número de zonas no problema inicial sem afetar sua largura combinada. Eventualmente, é identificado um ponto na esfera que não está coberto pelas zonas. Isso vai contra a hipótese de que a largura combinada das zonas é menor que π, provando a conjectura de Fejes Tóth.
 p Zonas que cobrem completamente uma esfera. Cada uma das cinco zonas tem sua própria largura e cor. Crédito:MIPT
p Zonas que cobrem completamente uma esfera. Cada uma das cinco zonas tem sua própria largura e cor. Crédito:MIPT
p O problema foi resolvido no espaço n-dimensional, mas os autores dizem que isso não o torna diferente do caso com três dimensões.
p "O problema de Fejes Tóth fascina matemáticos no campo da geometria discreta há mais de 40 anos, "diz o autor Alexandr Polyanskii do Departamento de Matemática Discreta, MIPT. "Este problema acabou por ter uma solução elegante, que tivemos a sorte de encontrar. O problema de Fejes Tóth nos levou a considerar outro, conjectura mais fundamental sobre a cobertura de uma esfera por zonas deslocadas definidas como a interseção da esfera com pranchas tridimensionais que não são necessariamente simétricas centralmente. "


