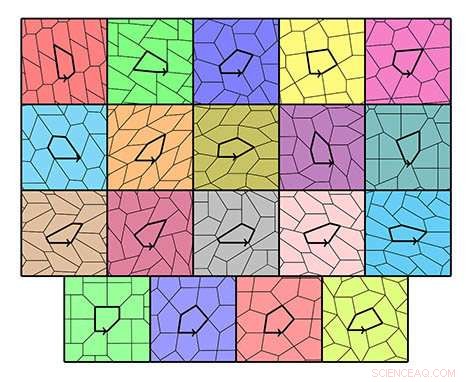
Os 15 tipos de ladrilhos pentagonais e seus 4 tipos específicos © Michael Rao, Laboratoire d'informatique du parallélisme. Crédito:CNRS / Inria / ENS Lyon / Université Claude Bernard Lyon
Ladrilhar o avião com um único padrão é um problema matemático que interessa aos humanos desde a Antiguidade, notadamente pela qualidade estética dos ladrilhos em mosaicos ou ladrilhos. Um dos problemas não resolvidos neste campo que tem intrigado a comunidade científica desde 1918 foi agora definitivamente resolvido graças a Michaël Rao do Laboratoire d'informatique du Parallélisme (CNRS / Inria / ENS de Lyon / Université Claude Bernard Lyon 1). Usando ferramentas de computação, ele foi capaz de demonstrar que existem apenas 15 padrões de cinco lados que podem lado a lado o avião. A pesquisa já está disponível no Arxiv local na rede Internet.
Existem várias soluções para revestir um piso com uma única forma, como triângulos, praças, retângulos, hexágonos, etc. A busca exaustiva por todas as formas convexas que podem telha o plano - uma forma com ângulos menores que 180 ° que podem cobrir uma parede inteira sem sobreposição - foi iniciada por Karl Reinhardt durante sua tese em 1918. Ele mostrou que todos os triângulos e os quadriláteros podem colocar o avião em blocos, mas que havia apenas 3 tipos de hexágonos que poderiam fazer isso, e que um polígono com sete lados ou mais não poderia fazer isso. Apenas a questão dos pentágonos permaneceu em aberto.
15 tipos de pentágonos foram descobertos de 1918 a 2015 como parte de uma pesquisa singular:iniciada por Reinhardt em 1918, passou por uma série de voltas e mais voltas, como novas descobertas de matemáticos amadores, até o anúncio midiatizado em 2015 de um novo 15º formulário 30 anos após o 14º. No entanto, a comunidade científica ainda não foi capaz de determinar se havia outras formas de pentágonos que poderiam revestir o avião.
Michaël Rao, pesquisador do CNRS no Laboratoire d'informatique du parallélisme (CNRS / Inria / ENS Lyon / Université Claude Bernard Lyon 1), agora demonstrou definitivamente que existe apenas uma série finita de famílias de pentágonos a serem levadas em consideração. Rao usou um programa de software para gerar todas as possibilidades, e mostrou que 371 famílias de pentágonos poderiam potencialmente revestir o avião. Ele então testou cada uma dessas famílias usando outro programa, e demonstrou que apenas 19 tipos de pentágonos atendiam às condições para ângulos e comprimentos laterais exigidos para ladrilhar o avião. Entre esses 19 tipos, 15 correspondiam a tipos já conhecidos, e os outros quatro provaram ser casos particulares desses 15 tipos. Consequentemente, apenas 15 tipos de ladrilhos podem colocar o avião em ladrilhos.
Rao foi capaz de resolver um problema centenário com sua metodologia, e para abrir novas perspectivas. Todos esses blocos convexos podem lado a lado o plano periodicamente (ou seja, as telhas se repetem infinitamente). No entanto, ainda não se sabe se existe um ladrilho que permite o revestimento não periódico. Felizmente, a maioria dessas técnicas também pode ser usada para polígonos não convexos, e poderia, assim, servir de base para a resolução de outro problema na área de ladrilhos, mais conhecido como o "Problema de Einstein" (do alemão "ein stein").