Desvendando erros posicionais e estruturais em modelos numéricos de previsão do tempo
 p Crédito CC0:domínio público
p Crédito CC0:domínio público
p Devido à natureza caótica da atmosfera, previsões do tempo, mesmo com modelos numéricos de previsão do tempo cada vez melhores, eventualmente perderá sua precisão. Os meteorologistas têm um grande desejo de entender melhor este processo, pois tentam rastrear o erro de previsão até as lacunas de observação e fornecer meios de melhoria. p Raiz do erro quadrático médio (rms, ou seu quadrado, a distância de variância) é freqüentemente usada para medir diferenças entre campos simulados e observados. Nesse caso, os cientistas mediram a distância entre um campo de previsão do modelo dentro de sua grade e o campo de análise de verificação que representa todas as observações do mundo real. Contudo, deve-se considerar que as características atmosféricas, assim como as frentes e os sistemas de pressão são características meteorológicas tridimensionais no espaço que os modelos de computador deslocam e também distorcem estruturalmente à medida que a previsão numérica se afasta do início. As métricas de variância ou erro rms não quantificam o deslocamento e a distorção dos sistemas meteorológicos.
p Em um artigo publicado recentemente em
Avanços nas Ciências Atmosféricas , uma equipe de cientistas da Administração Oceânica e Atmosférica Nacional (NOAA), o Instituto de Tecnologia de Massachusetts (MIT), e a Universidade de Connecticut decidiu encontrar uma abordagem geral para avaliar os componentes posicionais e estruturais da diferença total entre dois campos. Essencialmente, Os meteorologistas desejam avaliar a precisão de muitas características meteorológicas diferentes em um modelo de previsão em comparação com uma análise de verificação baseada em observações do mundo real.
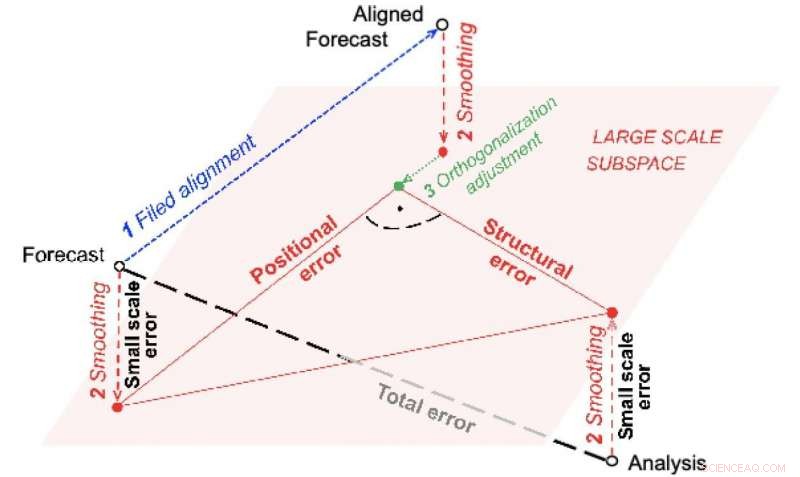 p Fig. 1. Esquema para redução total do erro de previsão:(1) Alinhe espacialmente uma previsão com o campo de análise de verificação; (2) Previsão e análise originais e alinhadas suaves para remover escalas imprevisíveis; (3) Decompor o erro total em componentes ortogonais (ângulo reto) de (i) erro posicional de grande escala, (ii) erro estrutural em grande escala, e (iii) ruído de pequena escala. Crédito:Isidora Jankov
p Fig. 1. Esquema para redução total do erro de previsão:(1) Alinhe espacialmente uma previsão com o campo de análise de verificação; (2) Previsão e análise originais e alinhadas suaves para remover escalas imprevisíveis; (3) Decompor o erro total em componentes ortogonais (ângulo reto) de (i) erro posicional de grande escala, (ii) erro estrutural em grande escala, e (iii) ruído de pequena escala. Crédito:Isidora Jankov
p Sai Ravela do MIT, um co-autor deste estudo, desenvolveu anteriormente um método de alinhamento de campo. Nesse caso, sua abordagem alinha o campo de previsão do modelo com a análise baseada na observação de uma maneira suave para que a diferença seja minimizada. Próximo, erros de pequena escala de origens incertas são removidos de todos os três campos (a previsão original e alinhada, bem como a análise de verificação, ou proxy para observações) por meio de um processo denominado filtragem espacial ou suavização. A distância de variância total, ou diferença, é então particionado em três componentes exclusivos. Erro de posição, que é a distância de variância entre a previsão do modelo original suavizada e os campos de previsão alinhados suavizados, e erro estrutural que é a distância de variância entre a previsão alinhada suavizada e os campos de análise de verificação suavizados, são dois lados de um triângulo retângulo, e ruído de escala fina, quais são os erros incertos de pequena escala removidos da previsão do modelo original e análise de verificação, ou campos de observação.
p Este método produz os três componentes de erro ortogonais como campos escalares, bem como um campo vetorial que indica o deslocamento em grande escala da previsão em relação ao campo de análise observacional. Interessantemente, em todas as regiões e prazos que a equipe estudou, mais da metade da variância total do erro está associada ao mau posicionamento das características meteorológicas. Portanto, o deslocamento é mais pronunciado do que a distorção nos campos de previsão:apenas cerca de 25% da variância do erro está associada a imprecisões estruturais das características parcialmente previsíveis, como frentes e sistemas de baixa pressão. O resto da variância do erro permanece variabilidade inexplicável ou imprevisível, ou ruído.
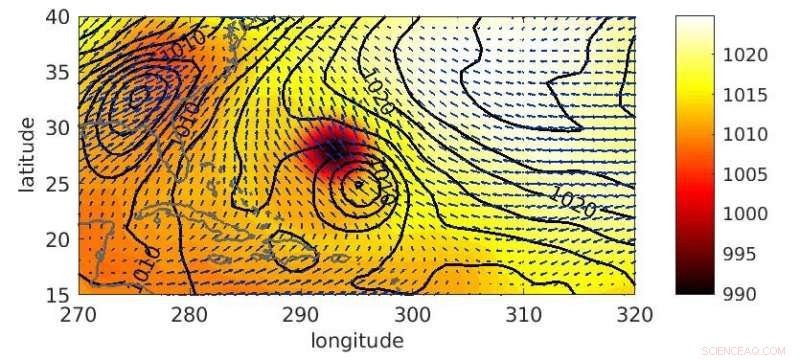 p Fig. 2. Previsão de 3,5 dias (contorno preto) e análise de verificação (tons de cor) da pressão média ao nível do mar para o furacão Katia, válido em 12 UTC, 6 de setembro de 2011. Mover a previsão junto com as setas azuis a alinha com a análise observacional. Crédito:Isidora Jankov
p Fig. 2. Previsão de 3,5 dias (contorno preto) e análise de verificação (tons de cor) da pressão média ao nível do mar para o furacão Katia, válido em 12 UTC, 6 de setembro de 2011. Mover a previsão junto com as setas azuis a alinha com a análise observacional. Crédito:Isidora Jankov
p "Como o ruído aumenta na variação do erro em função do tempo de espera da previsão, e se uma decomposição de ruído estrutural-posicional da propagação entre um conjunto de previsões perturbadas captura componentes de erro de previsão é o assunto de estudos em andamento, "disse o Dr. Jankov da NOAA, o principal autor do estudo.


