p Pesquisadores do QUT trabalhando em problemas complicados na agricultura, a ecologia e a medicina desenvolveram um modelo matemático para permitir soluções mais rápidas. p Perguntas sobre intervenção, quão forte e por quanto tempo, são apenas alguns dos julgamentos enfrentados por médicos e cientistas durante a tomada de decisões cotidiana.

p Da produção de safras à quimioterapia, nova pesquisa publicada em Interface do Jornal da Royal Society , melhora a forma de determinar as 'melhores' estratégias de intervenção.

p Professor Matthew Simpson, Ph.D. o pesquisador Jesse Sharp (foto à esquerda) e o professor Kevin Burrage do Centro de Ciência de Dados da QUT e do Centro Australiano de Excelência para Fronteiras Matemáticas e Estatísticas (ACEMS) desenvolveram o novo método matemático para simular mais rapidamente diferentes cenários para chegar a soluções ideais.

p Sr. Sharp, que está estudando seu Ph.D., disse que o método envolvia a teoria do controle ideal, que poderia ser descrita como uma "ciência das trocas" entre objetivos concorrentes.

p "O uso de técnicas de otimização matemática nos ajuda a tornar mais inteligente, decisões de alocação de recursos mais eficientes, " ele disse.

p "Se você der quimioterapia demais a alguém, você pode matar a leucemia e o paciente. Nesse caso, o 'custo' é obviamente muito alto, " ele disse.

p Ele disse que é importante encontrar o equilíbrio certo entre os benefícios da quimioterapia e os efeitos colaterais prejudiciais.

p "Você adivinha, execute esse cenário, use técnicas matemáticas para melhorar seu palpite repetidamente para chegar cada vez mais perto da solução ideal, " ele disse.

p "O que estamos fazendo é melhorar as técnicas numéricas, então você só precisa resolver esse problema menos vezes. "

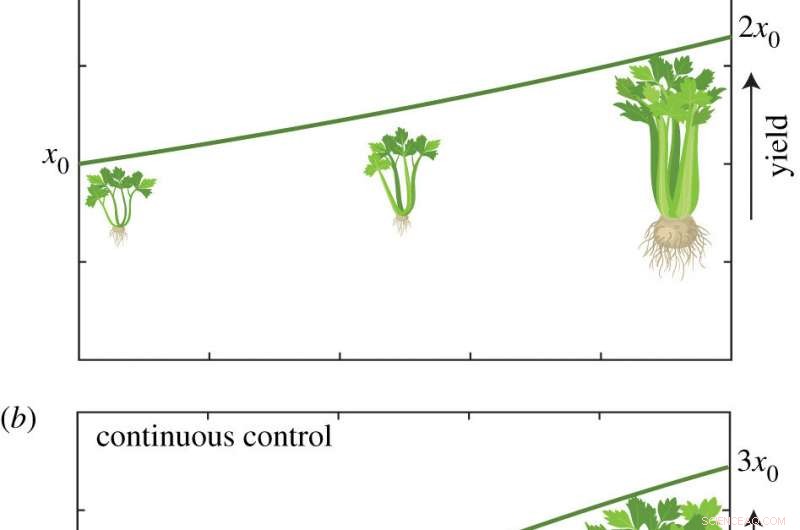
p O método também pode ser aplicado a práticas agrícolas (ver à esquerda), para exemplos na determinação de opções sobre como fertilizar plantações.

p A estratégia de controle ideal que surge para uma dada situação depende de como a otimização é caracterizada e o que o 'melhor resultado' significa no contexto da situação específica.

p O Sr. Sharp disse que a ilustração mostra "nenhum controle" como a estratégia mais simples, enquanto o controle 'bang bang' era uma intervenção que alternava entre o máximo e nenhum fertilizante, enquanto em 'controle contínuo, "o fertilizante pode ser aplicado em qualquer quantidade que pode mudar com o tempo.

p "Nesta pesquisa, melhoramos a eficiência das técnicas computacionais atualmente utilizadas para resolver esses problemas de otimização, " ele disse.

p "A maior eficiência pode nos permitir enfrentar problemas mais complexos que antes eram muito caros e demorados para resolver."

p O professor Matthew Simpson disse que a pesquisa pode ser aplicada a uma série de problemas.

p "Podemos encontrar uma solução mais rápido do que antes, ou podemos encontrar uma solução onde os métodos computacionais não conseguiram encontrar uma solução no passado, "Professor Simpson disse.

p "Sempre que você tem algum tipo de sistema para o qual deseja uma saída, então pode ser algo como um carro que dirige sozinho ou algum sistema biológico, esta é uma estratégia que pode indicar os protocolos ideais. "