 p Cubo de Rubik no estado resolvido. Crédito:Mike Gonzalez (TheCoffee)
p Cubo de Rubik no estado resolvido. Crédito:Mike Gonzalez (TheCoffee)
p O Cubo de Rubik é um dos quebra-cabeças favoritos do mundo há 40 anos. Vários métodos diferentes foram concebidos para resolvê-lo, conforme explicado em inúmeros livros. "Speedcubers" experientes podem resolvê-lo em questão de segundos. p Além de tais feitos de destreza surpreendente, existem muitas questões matemáticas fascinantes relacionadas ao Cubo de Rubik. Um movimento do cubo consiste em girar uma das seis faces em 90, 180, ou 270 graus. Um impressionante 43, 252, 003, 274, 489, 856, 000 estados possíveis podem ser obtidos aplicando sequências de movimentos ao estado resolvido.
p Apesar desta complexidade, foi mostrado em 2010 que o cubo de Rubik sempre pode ser resolvido em 20 movimentos ou menos, independentemente do estado inicial. Este número é conhecido como "o número de Deus, "já que todos os métodos de solução conhecidos usados por humanos normalmente usam significativamente mais movimentos do que esse valor ideal.
p Mas e quanto à pergunta oposta:quantos movimentos são necessários para embaralhar um cubo resolvido? À primeira vista, parece uma pergunta muito mais fácil do que calcular o número de Deus. Afinal, ao contrário de resolver um cubo, embaralhar um não requer nenhuma habilidade.
p Perguntas semelhantes foram respondidas com sucesso para embaralhamento de cartas. Um exemplo famoso é o estudo de 1990 do "riffle shuffle" pelos matemáticos Dave Bayer e Perci Diaconis. Um baralho de cartas é definido como "misto" se sua ordem for aleatória, com cada ordem possível tendo a mesma probabilidade de aparecer. Bayer e Diaconis mostraram que sete embaralhamentos de rifas são necessários e suficientes para misturar aproximadamente um baralho padrão de cartas de jogar.
p Ano passado, matemáticos publicaram um estudo semelhante do quebra-cabeça 15, que consiste em um quadrado 4x4 preenchido com 15 peças deslizantes e um espaço vazio.
 p Cubo de bolso em um estado embaralhado. Crédito:Mike Gonzalez (TheCoffee)
p Cubo de bolso em um estado embaralhado. Crédito:Mike Gonzalez (TheCoffee)
p
O que significa um cubo ser embaralhado?
p Uma pessoa típica tentando embaralhar um Cubo de Rubik executaria repetidamente movimentos aleatórios nele. A sequência aleatória de estados resultante é um caso especial do que os matemáticos chamam de cadeia de Markov. A propriedade principal é dada ao estado atual, a probabilidade de qual será o próximo estado não depende de nenhum dos estados anteriores.
p Aplicando a teoria das cadeias de Markov ao embaralhamento de cubos, segue-se que à medida que o número de movimentos aleatórios aumenta, a probabilidade de estar em qualquer um dos estados possíveis fica cada vez mais perto de 1/43, 252, 003, 274, 489, 856, 000. Os matemáticos chamam isso de "distribuição de probabilidade uniforme, "já que cada estado possível ocorre com a mesma probabilidade.
p Depois de qualquer número de movimentos aleatórios, o estado do cubo será aleatório, mas sua distribuição de probabilidade não será exatamente uniforme; alguns estados terão mais probabilidade de ocorrer do que outros.
p Deixar
d (t) descrever quanto a distribuição de probabilidade após
t movimentos aleatórios difere da distribuição de probabilidade uniforme. Conforme o número de movimentos aleatórios (
t ) aumenta, o valor de
d (t) diminuirá. O cubo sendo embaralhado corresponde a
d (t) sendo pequeno.
p
Cadeia de Markov Monte Carlo
p Na teoria das cadeias de Markov, esta diminuição em
d (t) é chamado de "mistura". Além de embaralhar cartas e quebra-cabeças, a teoria da mistura da cadeia de Markov também tem aplicações práticas muito sérias. Uma das ferramentas computacionais mais importantes na ciência e engenharia modernas é o método Monte Carlo. Este método, como o famoso cassino que leva o nome, depende fundamentalmente do acaso. Em essência, ele tenta resolver problemas matemáticos difíceis usando várias suposições aleatórias.
p Na prática, As cadeias de Markov são freqüentemente usadas para produzir esses estados aleatórios. Para entender a precisão desses métodos de Monte Carlo de cadeia de Markov, a tarefa principal é estimar a rapidez com que
d (t) diminui conforme
t aumenta.
p
O cubo de bolso
p Estudar o problema de embaralhamento do cubo de Rubik 3x3x3 padrão é atualmente um desafio fascinante não resolvido. Contudo, torna-se bastante gerenciável se voltarmos nossa atenção para uma versão menor 2x2x2, chamado de cubo de bolso.
p Neste cubo, a borda e as peças centrais estão ausentes e apenas as peças dos cantos permanecem. O cubo de bolso tem apenas 3, 674, 160 estados possíveis, e seu número de Deus é apenas 11.
p No gráfico abaixo, nós tramamos
d (t) para o cubo de bolso. Depois de 11 jogadas,
d (t) ainda é muito grande, em 0,695. O primeiro valor de
t que produz um
d (t) valor abaixo de 0,25 (muitas vezes chamado de "o tempo de mistura" na teoria da cadeia de Markov) é 19. Após 25 movimentos
d (t) é 0,092; após 50 movimentos, é 0,0012; e após 100 movimentos é 0,00000017.
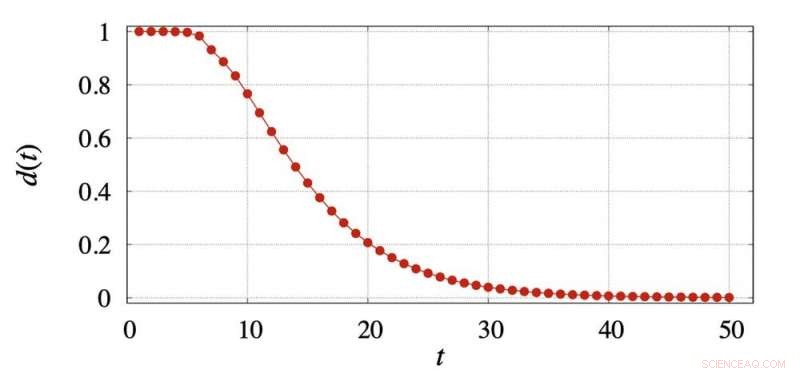 p Distância da distribuição do pocket cube do uniforme após t movimentos. Crédito:Eric Zhou
p Distância da distribuição do pocket cube do uniforme após t movimentos. Crédito:Eric Zhou
p
p Então, quantos movimentos você deve usar para embaralhar totalmente um cubo de bolso? A resposta depende de quão pequeno você gostaria
d (t) ser estar. Contudo, certamente é verdade que o número de movimentos de Deus é insuficiente. No mínimo, não se deve usar menos de 19 movimentos. Detalhes adicionais, incluindo código para calcular
d (t) , estão disponíveis aqui.
p E claro, uma vez que você embaralhou seu cubo, tudo o que resta a fazer é resolvê-lo novamente. p Este artigo foi republicado de The Conversation sob uma licença Creative Commons. Leia o artigo original.




