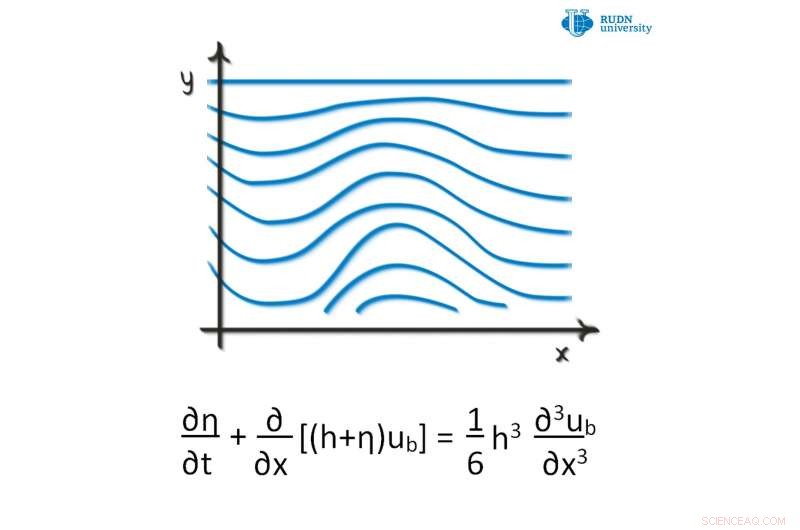
p Um matemático da Universidade RUDN propôs um novo critério para resolver as equações de Boussinesq. Essas equações descrevem a propagação não linear de ondas em certos meios, por exemplo. plasma, uma superfície de líquido de profundidade rasa, e assim por diante. Eles examinaram a equação de Boussinesq no espaço tridimensional e derivaram um critério para a unicidade e a existência de soluções importantes de um tipo especial para a equação diferencial parcial de Boussinesq. O critério proposto tem aplicações em mecânica de meios contínuos, que estuda o movimento de líquidos e gases. O artigo foi publicado em Boletim da Sociedade Brasileira de Matemática, Nova Série . p Ambas as equações de Boussinesq e de Navier-Stokes são sistemas de equações diferenciais parciais (a diferenciação é realizada em relação a todas as variáveis ​​independentes). Equações diferenciais parciais desempenham um papel significativo na física matemática e na mecânica. Resolver equações desse tipo costuma ser repleto de grandes dificuldades. O problema da existência e da singularidade de uma solução para as equações de Boussinesq sob determinadas condições iniciais (o chamado problema de Cauchy) havia sido investigado anteriormente por muitos cientistas, incluindo os autores do artigo. Com certos valores dos parâmetros, as equações de Boussinesq se transformam em equações de Navier-Stokes. A existência e diferenciabilidade contínua, ou, como dizem os matemáticos, Suavidade, de soluções para as equações de Navier-Stokes é um dos sete problemas do Prêmio Milênio, apresentado em 2000 pelo Clay Mathematics Institute.

p Para alguns espaços funcionais (nomeadamente, para espaços Besov homogêneos, pf que os famosos espaços de Sobolev são um caso especial), o problema foi resolvido com sucesso pelos matemáticos Don e Zhang. A matemática da Universidade RUDN Maria Alessandra Ragusa e sua colega foram mais longe, provando um critério semelhante para as equações de Boussinesq em espaços Besov homogêneos. Os autores examinaram as equações de Boussinesq no espaço tridimensional, o que possibilita uma aplicação mais completa dos resultados nas ciências naturais.

p Tendo introduzido uma série de definições necessárias e lemas auxiliares comprovados, o autor da RUDN University provou com sucesso o teorema principal e mostrou que a solução para o problema de Cauchy não só existe, é único, e não tem pontos singulares, mas também se estende suavemente a um intervalo maior de uma variável independente. O artigo usa o aparato de análise funcional, uma disciplina matemática com alto nível de abstração. No entanto, tais resultados podem encontrar ampla e frutífera aplicação na mecânica e na física.