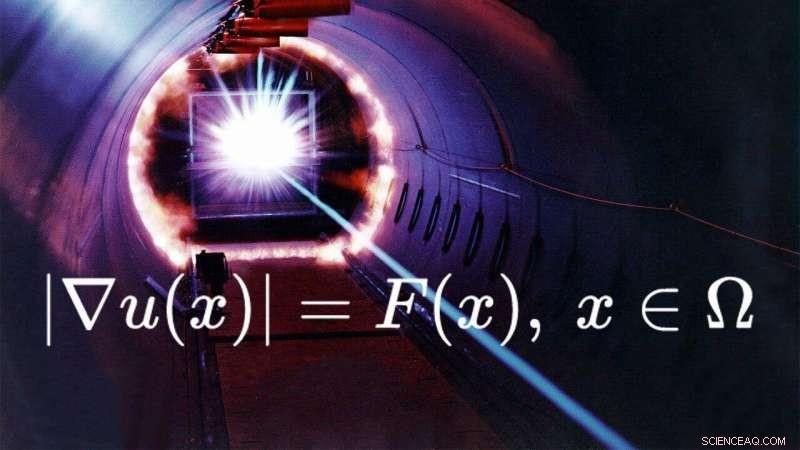Os matemáticos propuseram um método expresso para o cálculo da propagação da luz.
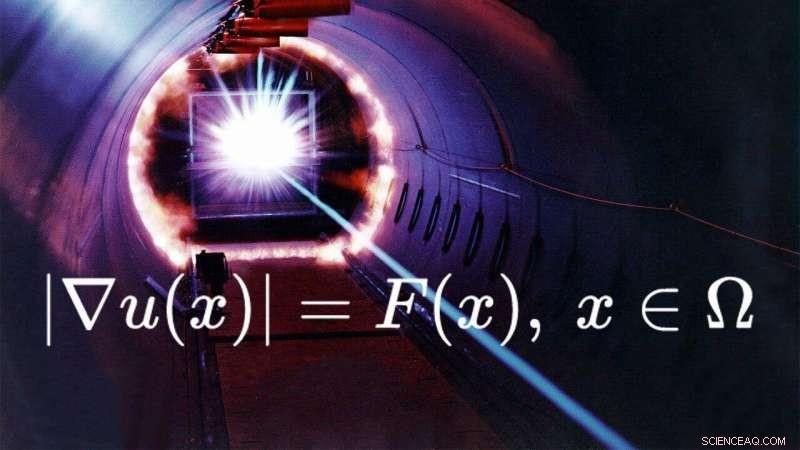 p Crédito:RUDN University
p Crédito:RUDN University
p Matemáticos da Universidade RUDN e do Instituto de Segurança Nuclear do RAS (NSI RAS) propuseram um método numérico para resolver equações que descrevem a propagação da luz em um meio. Eles usaram a equação eikonal não linear com as condições de contorno como base. Esse problema não pode ser resolvido diretamente, então os matemáticos desenvolveram um método numérico, cálculos realizados, e produziu uma imagem do "comportamento" de tais soluções. Os resultados podem se tornar a base para uma teoria abrangente de soluções aproximadas de tais equações diferenciais. O método pode ser aplicado na produção de lentes e cristais ópticos. O artigo foi publicado no
Journal of Computational and Applied Mathematics . p A equação eikonal é uma equação diferencial parcial não linear. Ele descreve a propagação da luz em um meio e é necessário para resolver problemas em óptica. Torna possível conectar a óptica plana, ensinado nas escolas, e óptica de ondas, que é descrito por equações complexas.
p É tradicional usar um método baseado na resolução de um grande sistema de equações não lineares para encontrar uma solução numérica (ou seja, para obter uma solução aproximada suficientemente precisa) para a equação eikonal.
p Os matemáticos da RUDN University e do NSI RAS usaram uma abordagem diferente, o que torna mais fácil encontrar uma solução para a equação eikonal não linear usando um método numérico:uma mudança de variáveis com a adição de um parâmetro. A mudança resulta em novas equações, que, por um lado, são mais simples do que os iniciais:o problema torna-se linear. Por outro lado, suas soluções não são as soluções do sistema original. Contudo, conforme o parâmetro diminui, as soluções para o novo sistema se aproximam das soluções para o original.
p Os matemáticos gradualmente (por um certo valor fixo) diminuíram o valor do parâmetro adicionado e para cada um desses valores resolveram a equação numericamente. Para cada valor de parâmetro subsequente, a solução resultante foi comparada com as anteriores. Conforme o parâmetro diminuiu, as soluções mudaram cada vez menos, isso é, o resultado dos cálculos estabilizou. Descobriu-se que uma solução suficientemente estável requer um valor de parâmetro relativamente pequeno. A solução resultante foi tomada como uma aproximação da equação original.
p Os matemáticos demonstraram que tal método produz resultados bastante bons em problemas de modelos representativos.
p "A complexidade computacional - os chamados 'custos computacionais' da abordagem da qual estamos falando - não excede a de outras abordagens. resolvemos um problema de valor limite linear, e essa, claro, é menos trabalhoso do que resolver um problema não linear, "explicou Petr Vabishevich, a autora do estudo e membro do Centro de Pesquisa em Métodos Computacionais em Matemática Aplicada da RUDN University.
p Vabishevich e seus co-autores modelaram a equação para meios anisotrópicos. Do ponto de vista da física, este é um ambiente no qual as propriedades físicas de propagação da luz em diferentes direções não são as mesmas. Materiais com essas propriedades são amplamente usados em dispositivos ópticos.
p Além da ótica, a equação eikonal também é usada para resolver numericamente equações que descrevem o movimento de um fluido. Essa modelagem é necessária para criar imagens realistas em computação gráfica - por exemplo, no filme "Piratas do Caribe", a água não foi apenas desenhada, mas calculada em um nível físico. A velocidade do cálculo, que poderia ser melhorado pelo método desenvolvido por matemáticos da RUDN University e NSI RAS, desempenha um papel fundamental em tais casos.