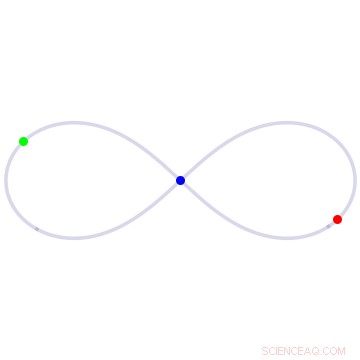
 p Na solução em forma de oito para o problema dos três corpos, três corpos de igual massa perseguem cada um em torno de um loop em forma de oito. Crédito:Universidade da Califórnia - Santa Cruz
p Na solução em forma de oito para o problema dos três corpos, três corpos de igual massa perseguem cada um em torno de um loop em forma de oito. Crédito:Universidade da Califórnia - Santa Cruz
p Desde suas origens, há mais de 300 anos, no trabalho de Newton em órbitas planetárias, o problema dos três corpos floresceu em um assunto rico que continua a produzir novos insights para os matemáticos. p Richard Montgomery, um distinto professor de matemática na UC Santa Cruz, chama isso de um dos dilemas clássicos da história da matemática. Em um artigo na edição de agosto da
Americano científico , ele relata a história do problema dos três corpos e o progresso que ele e outros matemáticos fizeram nas últimas duas décadas.
p "Ele desafiou as pessoas por séculos, e isso é parcialmente o que o torna interessante. Você está adicionando ao trabalho de pessoas como Newton e Poincaré e Lagrange, "Montgomery disse.
p O problema fundamental é prever os movimentos de três corpos (como estrelas ou planetas) atraídos mutuamente pela gravidade, dadas suas posições e velocidades iniciais. Acontece que uma solução geral para o problema é essencialmente impossível devido à dinâmica caótica, que Henri Poincaré descobriu em 1890.
p “Existem soluções para casos especiais, mas não há uma fórmula simples para lhe dar uma solução geral, "Montgomery explicou.
p Do ponto de vista prático de previsão de órbitas planetárias e planejamento de missões espaciais, aproximações podem ser calculadas com alto grau de precisão usando computadores e um processo chamado integração numérica. Isso pode ser bom o suficiente para a NASA, mas não para matemáticos, cujas explorações contínuas do problema levaram a avanços importantes na matemática.
p
Gatos caindo
p O problema de três corpos une três ramos diferentes da matemática:topologia, geometria, e dinâmica. Montgomery disse que foi isso que o interessou há mais de 20 anos. Ele estava trabalhando em questões relacionadas à matemática e à física de como um gato cai de pé, que tem aplicações em teoria de controle e orientação de satélites.
p "Continuei simplificando o problema até que o gato consistisse em apenas três pontos de massa, "Disse Montgomery. Então um colega o encaminhou a outro matemático que estava trabalhando em ideias semelhantes, e em pouco tempo ele mudou de gatos caindo para a mecânica celeste. Ao saber que as melhores pessoas que trabalhavam com mecânica celeste estavam em Paris, Montgomery passou um ano sabático lá trabalhando com Alain Chenciner na Universidade Paris Diderot no problema dos três corpos.
p Um de seus primeiros resultados importantes, publicado em 2000, foi uma redescoberta e prova de uma solução em forma de oito, em que três corpos de massa igual perseguem um ao outro indefinidamente em torno de um loop em forma de oito. Embora Chris Moore, do Santa Fe Institute, tenha encontrado essa solução pela primeira vez em 1993, usando um método de aproximação numérica, sua redescoberta por Montgomery e Chenciner teve um impacto muito maior no campo.
p "Fomos capazes de fornecer uma prova de existência rigorosa da solução do oito, e a forma como o fizemos permitiu que outros generalizassem a solução e encontrassem muitas outras coisas interessantes, "Montgomery explicou.
p Uma declaração mais geral do problema de três corpos para qualquer número de corpos maior que dois é chamada de problema de N-corpos. Montgomery disse quando apresentou pela primeira vez a solução em figura de oito com três corpos em uma conferência, um membro da platéia rapidamente apontou como deveria funcionar para quatro corpos. Breve, matemáticos estavam descobrindo um conjunto diversificado de novas órbitas para o problema de N-corpos de massa igual. Essas soluções periódicas em que todas as massas perseguem umas às outras em torno de um fixo, curva fechada sem colisões foram denominadas "coreografias" pelo matemático espanhol Carles Simó, quem descobriu centenas deles.
p "Criou uma mini-indústria, de modo que agora conhecemos um grande número dessas coreografias, "Montgomery disse.
p
Nova direção
p Anos depois, Simó ajudou a enviar a pesquisa de Montgomery sobre o problema dos três corpos em uma nova direção, sugerindo que ele procurasse mecanismos dinâmicos subjacentes às soluções periódicas. Isso levou a uma colaboração produtiva nos últimos anos com Rick Moeckel, da Universidade de Minnesota.
p As novas idéias matemáticas que surgiram do trabalho de Montgomery no problema dos três corpos não têm aplicações práticas, pelo menos não ainda. Frequentemente, conceitos matemáticos abstratos são desenvolvidos muito antes que alguém encontre um uso prático para eles.
p Muitas pessoas ficaram cativadas pelo apelo estético da solução em forma de oito e outras coreografias. O conceito chegou até mesmo à ficção científica através do autor chinês Liu Cixin, cujo romance The Three-Body Problem ganhou o Prêmio Hugo em 2015.
p Mas Montgomery diz que nunca teria enfrentado o problema se não tivesse mandato.
p "É um problema tão difícil, e você não sabe se vai fazer algum progresso, "disse ele." Mas a persistência compensa às vezes. Eu aprecio o sistema de posse, e também poder tirar licença sabática para trabalhar com colaboradores. Há algo sobre conhecer pessoas fisicamente que é tão importante para trabalharmos juntos. "
p No dele
Americano científico artigo, Montgomery fornece não apenas uma descrição detalhada do problema dos três corpos, mas também uma história fascinante das colaborações internacionais e relações pessoais que lhe permitiram fazer progressos neste enigma matemático convincente.
