 p Muitos estudos científicos não estão se segurando em novos testes. Crédito:fotografia A e N / Shutterstock.com
p Muitos estudos científicos não estão se segurando em novos testes. Crédito:fotografia A e N / Shutterstock.com
p Em um ensaio de um novo medicamento para curar o câncer, 44 por cento de 50 pacientes alcançaram remissão após o tratamento. Sem a droga, apenas 32 por cento dos pacientes anteriores fizeram o mesmo. O novo tratamento parece promissor, mas é melhor do que o padrão? p Essa pergunta é difícil, portanto, os estatísticos tendem a responder a uma pergunta diferente. Eles olham seus resultados e calculam algo chamado valor p. Se o valor p for menor que 0,05, os resultados são "estatisticamente significativos" - em outras palavras, improvável de ser causado apenas pelo acaso.
p O problema é, muitos resultados estatisticamente significativos não estão se replicando. Um tratamento que se mostra promissor em um ensaio não mostra nenhum benefício quando administrado ao próximo grupo de pacientes. Esse problema tornou-se tão grave que um jornal de psicologia realmente baniu os valores-p por completo.
p Meus colegas e eu estudamos esse problema, e achamos que sabemos o que está causando isso. O limite para reivindicar significância estatística é simplesmente muito baixo.
p
A maioria das hipóteses são falsas
p The Open Science Collaboration, uma organização sem fins lucrativos com foco em pesquisa científica, tentou replicar 100 experimentos psicológicos publicados. Enquanto 97 dos experimentos iniciais relataram descobertas estatisticamente significativas, apenas 36 dos estudos replicados o fizeram.
p Vários alunos de pós-graduação e eu usamos esses dados para estimar a probabilidade de que um experimento psicológico escolhido ao acaso testasse um efeito real. Descobrimos que apenas cerca de 7 por cento o fizeram. Em um estudo semelhante, a economista Anna Dreber e colegas estimaram que apenas 9% dos experimentos se replicariam.
p Ambas as análises sugerem que apenas cerca de um em cada 13 novos tratamentos experimentais em psicologia - e provavelmente em muitas outras ciências sociais - será um sucesso.
p Isso tem implicações importantes ao interpretar os valores p, principalmente quando estão perto de 0,05.
p
O fator Bayes
p Valores de P próximos a 0,05 são mais prováveis de serem devidos ao acaso do que a maioria das pessoas imagina.
p Para entender o problema, vamos voltar ao nosso ensaio imaginário de drogas. Lembrar, 22 de 50 pacientes com o novo medicamento entraram em remissão, em comparação com uma média de apenas 16 entre 50 pacientes no antigo tratamento.
p A probabilidade de obter 22 ou mais sucessos em 50 é de 0,05 se o novo medicamento não for melhor do que o antigo. Isso significa que o valor p para este experimento é estatisticamente significativo. Mas queremos saber se o novo tratamento é realmente uma melhoria, ou se não for melhor do que a velha maneira de fazer as coisas.
p Descobrir, precisamos combinar as informações contidas nos dados com as informações disponíveis antes de o experimento ser conduzido, ou as "probabilidades anteriores". As probabilidades anteriores refletem fatores que não são medidos diretamente no estudo. Por exemplo, eles podem ser responsáveis pelo fato de que em 10 outros ensaios de drogas semelhantes, nenhum provou ser bem-sucedido.
p Se o novo medicamento não for melhor do que o antigo, então, as estatísticas nos dizem que a probabilidade de ver exatamente 22 de 50 sucessos neste teste é de 0,0235 - relativamente baixa.
p E se o novo medicamento realmente for melhor? Na verdade, não sabemos a taxa de sucesso da nova droga, mas um bom palpite é que está perto da taxa de sucesso observada, 22 de 50. Se assumirmos isso, então, a probabilidade de observar exatamente 22 de 50 sucessos é 0,113 - cerca de cinco vezes mais provável. (Não quase 20 vezes mais provável, no entanto, como você poderia imaginar se soubesse que o valor p do experimento era 0,05.)
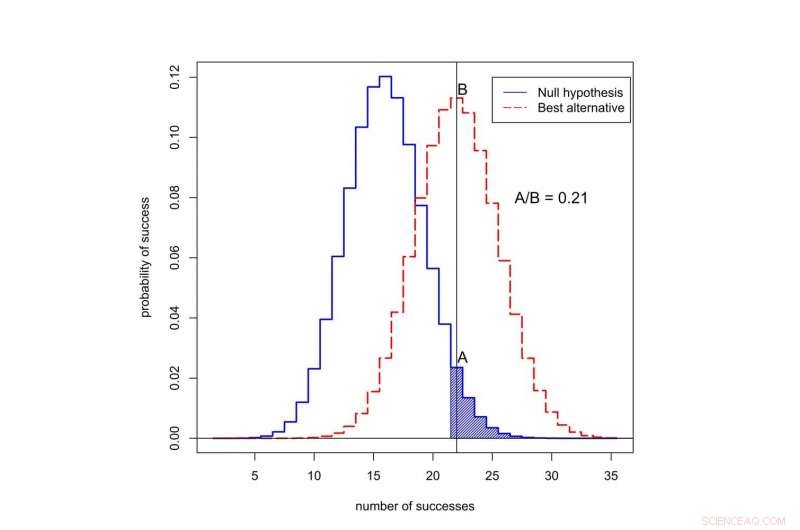 p Qual é a probabilidade de observar o sucesso em 50 tentativas? A curva preta representa probabilidades sob a 'hipótese nula, 'Quando o novo tratamento não é melhor do que o antigo. A curva vermelha representa as probabilidades de quando o novo tratamento é melhor. A área sombreada representa o valor p. Nesse caso, a proporção das probabilidades atribuídas a 22 sucessos é A dividido por B, ou 0,21. Crédito:Valen Johnson, CC BY-SA
p Qual é a probabilidade de observar o sucesso em 50 tentativas? A curva preta representa probabilidades sob a 'hipótese nula, 'Quando o novo tratamento não é melhor do que o antigo. A curva vermelha representa as probabilidades de quando o novo tratamento é melhor. A área sombreada representa o valor p. Nesse caso, a proporção das probabilidades atribuídas a 22 sucessos é A dividido por B, ou 0,21. Crédito:Valen Johnson, CC BY-SA
p Essa razão das probabilidades é chamada de fator de Bayes. Podemos usar o teorema de Bayes para combinar o fator de Bayes com as probabilidades anteriores para calcular a probabilidade de que o novo tratamento seja melhor.
p Para fins de argumentação, vamos supor que apenas 1 em 13 tratamentos experimentais contra o câncer seja um sucesso. Isso é próximo ao valor que estimamos para os experimentos de psicologia.
p Quando combinamos essas probabilidades anteriores com o fator de Bayes, Acontece que a probabilidade de o novo tratamento não ser melhor do que o antigo é de pelo menos 0,71. Mas o valor p estatisticamente significativo de 0,05 sugere exatamente o oposto!
p
Uma nova abordagem
p Essa inconsistência é típica de muitos estudos científicos. É particularmente comum para valores de p em torno de 0,05. Isso explica por que uma proporção tão alta de resultados estatisticamente significativos não se reproduz.
p Então, como devemos avaliar as alegações iniciais de uma descoberta científica? Em setembro, meus colegas e eu propusemos uma nova ideia:apenas valores P menores que 0,005 devem ser considerados estatisticamente significativos. Valores de p entre 0,005 e 0,05 devem ser meramente considerados sugestivos.
p Em nossa proposta, resultados estatisticamente significativos são mais propensos a se replicar, mesmo depois de levar em conta as pequenas probabilidades anteriores que normalmente pertencem aos estudos no social, ciências biológicas e médicas.
p O que mais, achamos que a significância estatística não deve servir como um limite positivo para publicação. Resultados estatisticamente sugestivos - ou mesmo resultados que são amplamente inconclusivos - também podem ser publicados, com base no fato de terem relatado ou não evidências preliminares importantes sobre a possibilidade de uma nova teoria ser verdadeira.
p Em 11 de outubro, apresentamos essa ideia a um grupo de estatísticos no Simpósio ASA sobre Inferência Estatística em Bethesda, Maryland. Nosso objetivo ao mudar a definição de significância estatística é restaurar o significado pretendido deste termo:os dados forneceram suporte substancial para uma descoberta científica ou efeito de tratamento.
p
Críticas à nossa ideia
p Nem todos concordam com nossa proposta, incluindo outro grupo de cientistas liderado pelo psicólogo Daniel Lakens.
p Eles argumentam que a definição dos fatores de Bayes é muito subjetiva, e que os pesquisadores podem fazer outras suposições que podem mudar suas conclusões. No ensaio clínico, por exemplo, Lakens pode argumentar que os pesquisadores poderiam relatar a taxa de remissão de três meses, em vez de seis meses, se forneceu evidências mais fortes a favor do novo medicamento.
p Lakens e seu grupo também acham que a estimativa de que apenas um em cada 13 experimentos se replicará é muito baixa. Eles apontam que esta estimativa não inclui efeitos como p-hacking, um termo para quando os pesquisadores analisam repetidamente seus dados até encontrar um valor p forte.
p Em vez de elevar o nível de significância estatística, o grupo Lakens acha que os pesquisadores devem definir e justificar seu próprio nível de significância estatística antes de conduzir seus experimentos.
p Eu discordo de muitas das afirmações do grupo Lakens - e, de uma perspectiva puramente prática, Eu sinto que a proposta deles não dá para começar. A maioria das revistas científicas não fornece um mecanismo para que os pesquisadores registrem e justifiquem sua escolha de valores-p antes de conduzirem os experimentos. Mais importante, permitir que os pesquisadores definam seus próprios limites de evidência não parece uma boa maneira de melhorar a reprodutibilidade da pesquisa científica.
p A proposta de Lakens só funcionaria se editores de periódicos e agências de financiamento concordassem com antecedência em publicar relatórios de experimentos que não foram conduzidos com base em critérios que os próprios cientistas impuseram. Eu acho que é improvável que isso aconteça em um futuro próximo.
p Até que aconteça, Eu recomendo que você não confie em afirmações de estudos científicos com base em valores de p próximos de 0,05. Insista em um padrão mais elevado. p Este artigo foi publicado originalmente em The Conversation. Leia o artigo original.



