Redes ou gráficos são descrições matemáticas da estrutura interna entre os componentes de um sistema complexo, como conexões entre neurônios, interações entre proteínas, contatos entre indivíduos em uma multidão, e interações entre usuários em plataformas sociais online. Os links na maioria das redes reais mudam com o tempo, e essas redes são freqüentemente chamadas de redes temporais. A temporalidade dos links codifica a ordem e causalidade das interações entre os nós e tem um efeito profundo na função da rede neural, propagação de doenças, agregação de informações e recomendação, surgimento de comportamento cooperativo, e controlabilidade da rede. O aumento da pesquisa tem se concentrado em explorar os padrões em uma rede temporal e prever sua evolução futura usando técnicas de aprendizado de máquina, especialmente redes neurais de gráfico. Contudo, como quantificar o limite de previsibilidade de uma rede temporal, ou seja, o limite que nenhum algoritmo pode ultrapassar, ainda é uma questão em aberto.

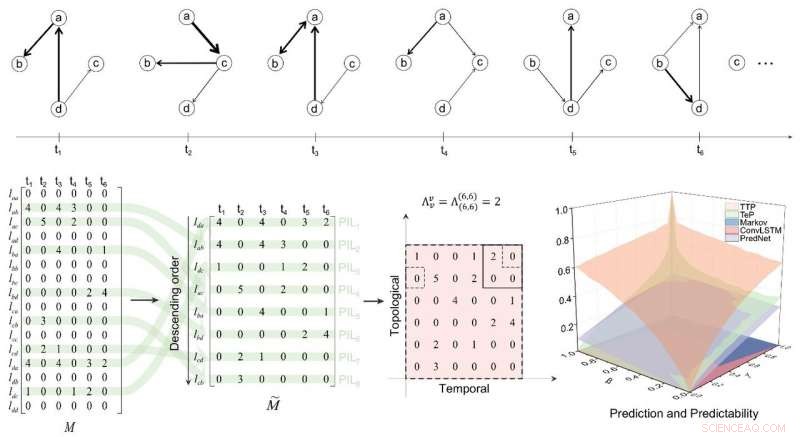
Recentemente, uma equipe de pesquisa liderada por Xianbin Cao com a Universidade Beihang, Pequim, e Gang Yan na Universidade de Tongji, Xangai, publicou um artigo intitulado "Previsibilidade de redes temporais reais" em National Science Review e propôs um framework para quantificar a previsibilidade de redes temporais com base na taxa de entropia de campos aleatórios.

Os autores mapearam qualquer rede dada a uma matriz temporalidade-topologia, e então estendeu o cálculo clássico da taxa de entropia (que só é aplicável a matrizes quadradas) para matrizes arbitrárias por meio de operadores de regressão. As vantagens significativas dessa previsibilidade temporal-topológica foram validadas em dois modelos típicos de redes temporais. Aplicando o método para calcular a previsibilidade de 18 redes reais, os autores descobriram que em diferentes tipos de redes reais, as contribuições da topologia e temporalidade para a previsibilidade da rede são significativamente variáveis; Embora a linha de base teórica e a dificuldade de previsibilidade topológica temporal sejam muito maiores do que as séries temporais unidimensionais, as previsibilidades temporal-topológicas da maioria das redes reais ainda são maiores do que as séries temporais.

O limite de previsibilidade calculado nesta pesquisa é uma propriedade intrínseca das redes temporais, ou seja, é independente de qualquer algoritmo preditivo, portanto, também pode ser usado para medir o espaço possível de aprimoramento de algoritmos preditivos. Os autores examinaram três algoritmos preditivos amplamente usados ​​e descobriram que o desempenho desses algoritmos é significativamente menor do que os limites preditivos na maioria das redes reais, sugerindo a necessidade de novos algoritmos preditivos que levem em consideração as características temporais e topológicas das redes.