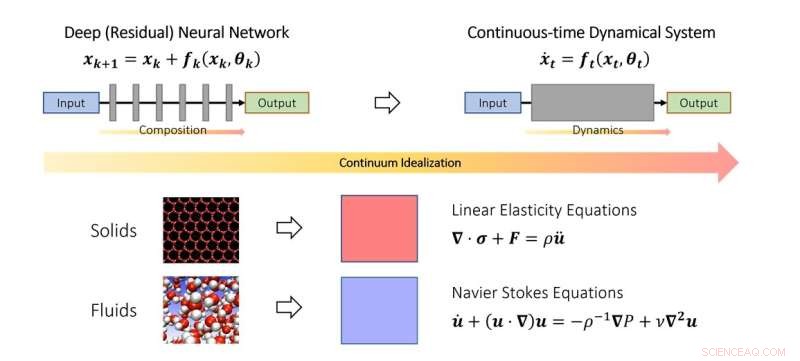
O ponto de vista contínuo do aprendizado profundo. Semelhante a como os cientistas estudam a mecânica de sólidos e fluidos no limite do contínuo, também se pode idealizar redes neurais profundas como uma discretização de um sistema dinâmico contínuo. No esquema, o parâmetro de tempo fictício representa um análogo contínuo de camadas e a dinâmica modela o empilhamento de camadas. Crédito:Qianxiao Li
Os matemáticos da NUS desenvolveram uma nova estrutura teórica baseada em sistemas dinâmicos para entender quando e como uma rede neural profunda pode aprender relacionamentos arbitrários.
Apesar de alcançar sucesso generalizado na prática, entender os princípios teóricos do aprendizado profundo continua sendo uma tarefa desafiadora. Uma das questões mais fundamentais é:as redes neurais profundas podem aprender relações arbitrárias de entrada-saída (em matemática, elas são chamadas de funções) e a maneira como elas alcançam isso difere das metodologias tradicionais?
Para entender essa questão, é necessário pensar sobre o que exatamente há de novo nas redes neurais profundas em comparação com os paradigmas tradicionais de aproximação de funções. Por exemplo, a série clássica de Fourier aproxima funções complicadas como uma soma ponderada de funções mais simples, como senos e cossenos. As redes neurais profundas operam de maneira bastante diferente. Em vez de somas ponderadas, eles constroem funções complexas a partir do empilhamento repetido de funções simples (camadas). Isso também é conhecido como composição de funções em matemática. A questão-chave é como funções complicadas podem ser construídas a partir de funções simples, empilhando-as juntas. Acontece que este é um problema bastante novo no ramo da matemática conhecido como teoria da aproximação.
Neste estudo publicado no
Journal of the European Mathematical Society , Professor Assistente Qianxiao LI do Departamento de Matemática da Universidade Nacional de Cingapura e seus colaboradores desenvolveram uma nova teoria das capacidades de aproximação da composição de funções. Uma observação interessante é que, embora a composição de funções seja difícil de analisar na prática devido à sua estrutura discreta e não linear, esta não é a primeira vez que ocorrem tais problemas.
No estudo do movimento de sólidos e fluidos, eles são frequentemente idealizados como um continuum de partículas, satisfazendo algumas equações contínuas (equações diferenciais ordinárias ou parciais). Isso permite que a dificuldade de modelar tais sistemas no nível atômico discreto seja contornada. Em vez disso, foram derivadas equações contínuas que modelam seu comportamento no nível macroscópico.
A ideia chave do estudo é que este conceito pode ser estendido para redes neurais profundas, idealizando a estrutura em camadas como um sistema dinâmico contínuo. Isso conecta o aprendizado profundo com o ramo da matemática conhecido como sistemas dinâmicos. Tais conexões permitem o desenvolvimento de novas ferramentas para entender a matemática da aprendizagem profunda, incluindo uma caracterização geral de quando ela pode de fato aproximar relações arbitrárias.
O professor Li disse:"O ponto de vista de sistemas dinâmicos de aprendizado profundo oferece uma estrutura matemática promissora que destaca os aspectos distintivos das redes neurais profundas em comparação com os paradigmas tradicionais. Isso traz novos problemas matemáticos interessantes na interface de sistemas dinâmicos, teoria de aproximação e aprendizado de máquina. "
“Uma área promissora de desenvolvimento futuro é estender essa estrutura para estudar outros aspectos das redes neurais profundas, como treiná-las efetivamente e como garantir que funcionem melhor em conjuntos de dados invisíveis”, acrescentou o professor Li.
+ Explorar mais A rede neural racional avança no aprendizado de equações de diferenciação parcial
