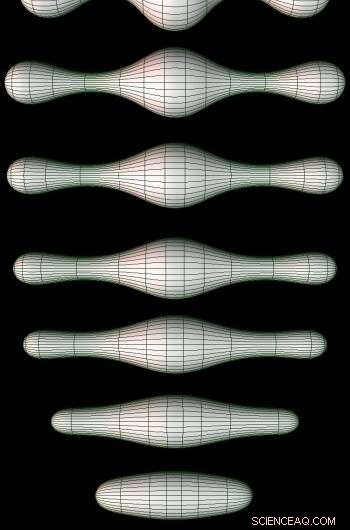
 p Os estágios serval de Ricci Flow em um manifold 2D. Crédito:https://en.wikipedia.org/wiki/Ricci_flow
p Os estágios serval de Ricci Flow em um manifold 2D. Crédito:https://en.wikipedia.org/wiki/Ricci_flow
p A geometria diferencial é o estudo da geometria espacial. Vários fenômenos naturais, da expansão universal à expansão e contração térmica, pode se resumir à evolução espacial. As duas conjecturas centrais neste campo, a conjectura de Hamilton-Tian e o C parcial
0
conjetura, foram quebra-cabeças não resolvidos por mais de 20 anos. p "A maioria dos seixos da praia são redondos. Eles podem ter bordas e cantos no início, mas conforme o tempo passa e a maré vai e vem, sua forma ficará cada vez mais próxima da perfeição e do padrão. Mas não importa o quão perfeita seja a evolução, ainda pode haver algumas anormalidades, que são chamados de 'singularidades' em geometria. "
p "A conjectura de Hamilton-Tian sugere que a maior parte do espaço é perfeito, enquanto o tamanho da 'singularidade' pode ser restrito a um espaço de baixa dimensão, "disse o Prof. Chen Xiuxiong, o fundador do Instituto de Geometria e Física, Universidade de Ciência e Tecnologia da China (USTC) da Academia Chinesa de Ciências (CAS).
p Prof Chen, juntamente com o Prof. Wang Bing da USTC, primeiro provou as duas conjecturas.
p O artigo foi dividido em 123 páginas em duas partes de, o primeiro deles foi publicado em 2017 e o segundo este ano em
Journal of Differential Geometry , que também publicou o trabalho fundamental de Hamilton sobre o fluxo de Ricci após um longo curso de cinco anos de desenvolvimento da teoria e seis anos de revisão por pares desde sua primeira apresentação.
p Este trabalho enfatizou a teoria de compactação fraca para escoamentos de Ricci não colapsados. Introduziu muitos pensamentos e métodos inovadores, que contribuiu com implicações de longo alcance no campo da análise geométrica, especialmente para os estudos de fluxos de Ricci.
p Na verdade, muitos outros trabalhos foram desenvolvidos com base neste artigo. Por exemplo, uma nova solução para a estabilidade da conjectura de Yau baseada na teoria da estrutura dos fluxos de Ricci foi dada pelo Prof. Chen, Prof. Wang e Dr. Sun Song da USTC com sua derivação publicada em
Geometria e Topologia . Antes disso, eles receberam o Prêmio Oswald Veblen de Geometria pela primeira solução para a estabilidade da conjectura de Yau.
p A teoria e os métodos apresentados neste artigo também foram aplicados em uma série de trabalhos do Prof. Wang e seus colaboradores nos últimos anos.
p As ideias centrais deste artigo foram generalizadas para a pesquisa do fluxo de curvatura média pelo Prof. Wang e Prof. Li Haozhao, quem resolveu o problema da extensão, e o resultado foi publicado em
Invenções Mathematicae .
p O artigo do Prof. Wang, Dr. Huang Shaosai e Dr. Li Yu, "Sobre a convexidade regular dos espaços limite do encolhedor de Ricci, " publicado em
Crelle's Journal , provou que o limite de solitons de Ricci com encolhimento não colapsado deve ser o formato de cone definido pelo Prof. Chen e pelo Prof. Wang.
p Adicionalmente, o artigo "Heat Kernel on Ricci Shrinkers, " publicado em
Cálculo de variações e equações diferenciais parciais pelo Prof. Wang e Dr. Li, desenvolveu várias estimativas por meio do estudo do núcleo de calor em redutores de Ricci e forneceu "ferramentas necessárias para analisar singularidades de curto tempo dos fluxos de Ricci de dimensão geral".
p Essa descoberta foi homenageada pelo revisor da revista e vencedor do Fields Metal, Prof. Simon Donaldson, quem disse, "este trabalho é um grande avanço na análise geométrica, e sem dúvida conduzirá muitos outros projetos de pesquisa relacionados. "
