
Crédito:MarcoVector / Shutterstock
As doenças afligem os humanos desde que existem humanos. Acredita-se que a malária e a tuberculose tenham devastado o Egito Antigo mais de 5, 000 anos atrás. De 541 a 542 DC, estima-se que a pandemia global conhecida como "a Peste de Justiniano" tenha matado de 15 a 25% da população mundial de 200 milhões. Após a conquista espanhola do México, a população nativa caiu de cerca de 30 milhões em 1519 para apenas três milhões 50 anos depois. Hoje estamos lutando para controlar a disseminação do COVID-19, que tem o potencial de causar a pandemia mais mortal da história humana.
Há, Contudo, um campo da ciência pouco conhecido, mas muito bem-sucedido, trabalhando em segundo plano para desvendar os mistérios das doenças infecciosas. Conforme eu exploro em The Maths of Life and Death, A epidemiologia matemática desempenha um papel crucial na luta contra doenças infecciosas de grande escala, como a COVID-19.
Com modelos matemáticos básicos, os pesquisadores podem começar a prever a progressão das doenças e compreender o efeito das intervenções na propagação das doenças. Com modelos mais complexos, podemos começar a responder a perguntas sobre como alocar de forma eficiente recursos limitados ou descobrir as consequências das intervenções de saúde pública, como fechar pubs e proibir reuniões.
Os insights da modelagem matemática são vitais para garantir que as autoridades possam prevenir o maior número possível de mortes. À medida que a pandemia COVID-19 aumenta, aqui está uma olhada dentro da modelagem que os especialistas usam para tentar ficar um passo à frente do vírus.
O modelo S-I-R
Um dos modelos matemáticos mais simples de propagação de doenças divide a população em três categorias básicas de acordo com o estado da doença. Pessoas que ainda não tiveram a doença são rotuladas de "suscetíveis". Presume-se que todas as pessoas nascem suscetíveis e capazes de ser infectadas. Aqueles que contraíram a doença e são capazes de transmiti-la aos suscetíveis são os "infecciosos". O terceiro grupo é eufemisticamente referido como a classe "removida". Estas são as pessoas que tiveram a doença e se recuperaram e agora estão imunes, ou aqueles que morreram. Esses indivíduos "removidos" não contribuem mais para a disseminação da doença.
Isso é conhecido como modelo S-I-R. Da dengue na América Latina à febre suína na Holanda e norovírus na Bélgica, o modelo S-I-R pode fornecer lições vitais sobre como prevenir a propagação de doenças.
Este modelo ilustra a importância do isolamento social para as pessoas infectadas. Ao ficar em casa até a recuperação completa, você efetivamente sai da classe infectada direto para a classe removida, sem contrair o vírus. Essa ação simples pode reduzir o tamanho de um surto, reduzindo as oportunidades de transmissão da doença a indivíduos suscetíveis.
O fato de um surto se espalhar ou morrer é amplamente ditado por um único número que é exclusivo daquele surto - o número de reprodução básico.
Pense em uma população que é completamente suscetível a uma doença específica, bem como a população global em dezembro de 2019, no início do surto COVID-19. O número médio de indivíduos não expostos anteriormente infectados por um único, O portador da doença recentemente introduzida é conhecido como o número básico de reprodução, e frequentemente denotado R₀ (pronuncia-se "R-nada" ou "R-zero").
Se uma doença tiver um R₀ menor que um, então a infecção morrerá rapidamente à medida que cada pessoa infecciosa passa a doença, na média, para menos de um outro indivíduo. O surto não pode sustentar sua própria propagação. Se R₀ for maior que um, o surto aumentará exponencialmente.
Explosão exponencial
As primeiras estimativas do número de reprodução básica para COVID-19 colocam-no em algum lugar entre 1,5 e 4, com um valor de pelo menos 2 em dezembro e janeiro. Com um número de reprodução básico de 2, a primeira pessoa com a doença a espalha para outras duas, quem cada, na média, espalhar a doença para outras duas pessoas e, em seguida, para outras duas cada, e assim por diante.
Esse crescimento exponencial é característico da fase inicial da infecção. Se a propagação pudesse continuar assim, dez gerações abaixo da cadeia de progressão, acima de 1, 000 pessoas seriam infectadas. Dez passos adiante, o número aumentaria para mais de um milhão.
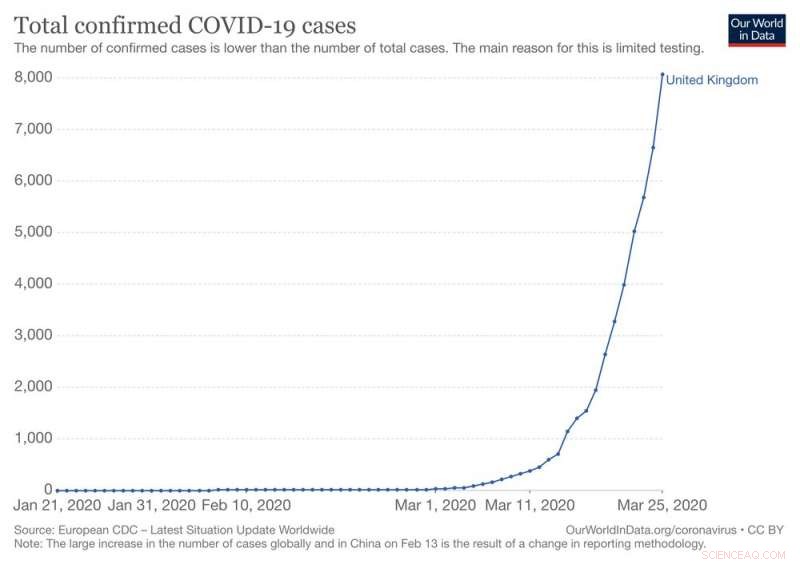
Novos casos de COVID-19 no Reino Unido mostraram um aumento exponencial nos últimos dias. Crédito:Max Roser, Hannah Ritchie e Esteban Ortiz-Ospina (2020) - 'Doença do Coronavírus (COVID-19) - Estatísticas e Pesquisa', CC BY
Na prática, o crescimento exponencial previsto pelo número de reprodução básico raramente é sustentado além de algumas gerações. Os surtos eventualmente chegam ao pico e depois diminuem devido à diminuição da frequência de contatos entre infectivos e suscetíveis.
Mesmo quando não há mais infecciosos e o surto está oficialmente encerrado, alguns suscetíveis permanecerão. O modelo S-I-R pode fornecer uma estimativa do tamanho final da epidemia - o número de pessoas infectadas no final de um surto se nenhuma ação corretiva for tomada. Na extremidade inferior das estimativas para COVID-19, um número de reprodução de 1,5, significa que 58% da população seria infectada. Na extremidade superior das estimativas, com um R₀ de 4, o modelo S-I-R prevê que apenas 2% das pessoas permaneceriam não infectadas se nenhuma ação fosse tomada.
Um número crucial
O número de reprodução básico é útil para a compreensão de quase todos os surtos, porque agrupa todas as sutilezas da transmissão de doenças em uma única figura. Da maneira como a infecção se desenvolve no corpo, ao modo de transmissão - e até mesmo à estrutura das sociedades nas quais se espalha - ele captura todas as características-chave do surto e nos permite reagir de acordo.
R₀ normalmente pode ser dividido em três componentes:o tamanho da população, a taxa na qual os suscetíveis são infectados (muitas vezes conhecida como a força da infecção), e a taxa de recuperação ou morte da doença. Aumentar os dois primeiros desses fatores aumenta R₀, enquanto o aumento da taxa de recuperação a reduz. Quanto maior a população e mais rápido a doença se espalha entre os indivíduos, maior será a probabilidade de o surto ser. Os indivíduos mais rápidos se recuperam, menos tempo eles têm para passar a doença para outras pessoas e, consequentemente, mais fácil será controlar um surto.
Então há o eficaz número de reprodução. Este é o número médio de infecções secundárias causadas por um indivíduo infeccioso em um determinado ponto da progressão do surto. Se, por intervenção, o número de reprodução efetiva pode ser inferior a um, então a doença morrerá.
Taxa de mortalidade de casos
Embora crucial para o controle da doença, R₀ não nos diz a gravidade de uma doença para um indivíduo infectado. A proporção de pessoas infectadas que morrem de uma doença é conhecida como taxa de letalidade.
Uma doença extremamente infecciosa como o sarampo, com um R₀ entre 12 e 18, tem uma taxa de letalidade relativamente baixa em comparação com os 50-70% dos pacientes com Ebola que acabarão morrendo da doença. Como resultado, O sarampo é normalmente considerado menos grave do que o Ebola, embora o Ebola tenha um R₀ muito menor, de cerca de 1,5. As primeiras estimativas indicam que a taxa de letalidade do COVID-19 está entre 0,25% e 3,5%.
É importante lembrar que a taxa de letalidade não é fixa - depende das respostas da sociedade e dos indivíduos à doença, bem como na demografia da população que infecta. Por exemplo, as taxas de letalidade para COVID-19 parecem variar significativamente com a idade do paciente, com os idosos sendo os mais afetados.
Talvez surpreendentemente, doenças com altas taxas de letalidade tendem a ser menos infecciosas. Se uma doença mata muitas de suas vítimas muito rapidamente, ela reduz suas chances de ser transmitida. Doenças que matam a maioria das pessoas que infectam e também se espalham com eficiência são muito raras, e geralmente se limitam a filmes de desastre.
Embora uma alta taxa de letalidade aumente significativamente os temores durante um surto, doenças com alto R₀, mas letalidade em minúsculas (pense no COVID-19 em comparação ao Ebola) podem acabar matando mais pessoas em virtude do maior número que infectam.
Controlando um surto
Uma das opções mais eficazes para reduzir a propagação da doença é a vacinação. Ao levar as pessoas diretamente de suscetíveis para removidas, contornando o estado infeccioso, efetivamente reduz o tamanho da população suscetível.
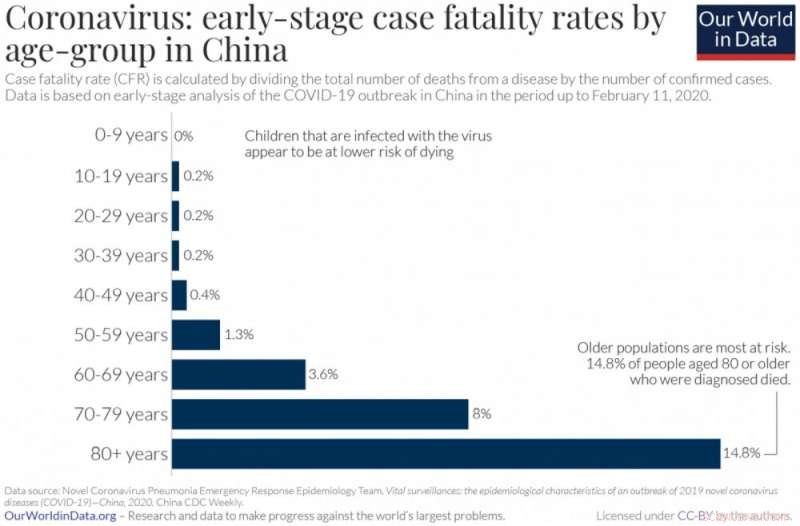
Os idosos têm maior probabilidade de morrer de COVID-19 do que a população como um todo. Crédito:Max Roser, Hannah Ritchie e Esteban Ortiz-Ospina (2020) - 'Doença do Coronavírus (COVID-19) - Estatísticas e Pesquisa', CC BY
Mas a vacinação é tipicamente uma medida de precaução usada para reduzir a probabilidade de surtos acontecerem. Assim que surtos como a atual pandemia COVID-19 estiverem em pleno andamento, muitas vezes é impraticável desenvolver e testar uma vacina em um período de tempo útil.
Quarentena e isolamento podem reduzir com eficiência a taxa de transmissão e, consequentemente, o número de reprodução efetiva. O isolamento de pacientes infecciosos reduz a taxa de disseminação, enquanto a quarentena de indivíduos saudáveis reduz a população suscetível efetiva.
Ambas as ações contribuem para diminuir o número de reprodução efetiva, razão pela qual o distanciamento social e o auto-isolamento são estratégias tão importantes para lidar com o COVID-19.
Imunidade de rebanho
Uma ideia com a qual o governo do Reino Unido parecia estar brincando nos primeiros dias de sua resposta era a imunidade de rebanho - o conceito de que uma grande população de indivíduos imunes pode retardar ou mesmo interromper a propagação da doença. Surpreendentemente, esse efeito comunitário não exige que todos sejam imunes à doença para que toda a população seja protegida. Ao reduzir o número de reprodução efetiva para menos de um - garantindo que as pessoas infectadas entrem em contato com o menor número possível de pessoas suscetíveis - a cadeia de transmissão pode ser interrompida e a doença interrompida. Crucialmente, imunidade de rebanho significa que as pessoas imunocomprometidas, os idosos, mulheres grávidas e outros grupos demográficos de alto risco podem se beneficiar da proteção proporcionada pela imunidade de outras pessoas.
A fração da população que precisa ser imune para proteger o resto varia dependendo de quão infecciosa é a doença. O número básico de reprodução, R₀, é a chave de quão grande é essa proporção. Quanto maior o número de reprodução básica, quanto maior a proporção imune da população precisa ser. Por exemplo, para uma doença com um número de reprodução básico de 4, o modelo S-I-R prevê que três quartos da população devem ser imunes. Se R₀ for tão baixo quanto 1,5, então, potencialmente, apenas um terço da população precisa adquirir imunidade para proteger os dois terços restantes.
Se uma vacina estiver disponível, então a imunidade do rebanho pode ser alcançada pela vacinação de uma proporção suficientemente alta da população (que disse, apenas conseguimos erradicar completamente uma doença humana - a varíola - por meio da vacinação).
Quando uma vacina não estiver disponível, a única maneira de as pessoas adquirirem imunidade é infectando-se com a doença e se recuperando. Dada a taxa de mortalidade de casos de COVID-19, isso acarretaria a morte de muitos milhares de pessoas. Sem surpresa, o governo do Reino Unido voltou atrás em sua política proposta.
A próxima geração de modelagem
Na realidade, o modelo S-I-R simples não é complexo o suficiente para capturar as sutilezas de muitos surtos de doenças infecciosas. Mas para doenças que não conferem imunidade às suas vítimas, uma simples adaptação do modelo S-I-R pode ajudar.
Como é típico de algumas doenças sexualmente transmissíveis, a gonorréia não removeu nenhuma população. Uma vez recuperado da gonorréia, os pacientes podem ser infectados novamente. Uma vez que ninguém morre com os sintomas da gonorréia, ninguém nunca é "removido" da população. Esses modelos são normalmente rotulados S-I-S, imitando o padrão de progressão de um indivíduo de suscetível a infeccioso e de volta a suscetível novamente. Uma vez que a população de pessoas suscetíveis nunca se esgota, mas renovado conforme as pessoas se recuperam, o modelo S-I-S prevê que as doenças podem se tornar autossustentáveis ou "endêmicas".
Se uma única infecção pelo SARS-CoV-2 (o vírus que causa o COVID-19) foi suficiente para fornecer imunidade foi uma das principais preocupações dos cientistas no início do surto. O novo vírus poderia circular indefinidamente na população? Embora tenha havido vários relatos de pessoas pegando o vírus pela segunda vez, também há boas evidências que sugerem que os pacientes com COVID-19 recuperados tornam-se imunes.
Outro problema com o novo coronavírus é que normalmente há um período assintomático no início da doença. Durante este tempo, as pessoas podem abrigar o vírus e infectar outras sem apresentarem sintomas. Isso significa que precisamos adicionar outra classe de pessoas ao modelo. Estas são pessoas que, uma vez infectado, são capazes de transmitir a doença sem apresentar sintomas - a chamada classe de "portadores". Isso muda o modelo S-I-R em um modelo S-C-I-R. A classe de portadores é vital para representar doenças como HIV / AIDS, que apresentam longos períodos infecciosos sem sintomas evidentes.
Os modelos de última geração que estão sendo usados atualmente para informar a política governamental são ainda mais complicados. Infelizmente, mesmo o mais detalhado e realista dos modelos matemáticos não é capaz de prever quando a atual pandemia chegará ao fim.
Mas é certo que, quando eventualmente assumimos o controle da situação, os matemáticos e seus modelos terão desempenhado um papel significativo na maneira como o drama se desenrolou.
Este artigo foi republicado de The Conversation sob uma licença Creative Commons. Leia o artigo original. 