p Matemáticos da Universidade RUDN estudaram as propriedades dos operadores composicionais em espaços com normas de Lebesgue mistas. Seu trabalho ajudará a descrever a difusão de líquidos em materiais com fissuras e em materiais porosos. Esses espaços também são úteis para obter estimativas de soluções para a equação de Navier-Stokes. O artigo foi publicado em Notas Matemáticas . p A ciência moderna das equações diferenciais parciais tem sua própria teoria:a linguagem da análise funcional. Os estudos de espaços funcionais nos quais se buscam soluções para equações começaram no século 19 e continuaram até o presente. Inicialmente, matemáticos aprenderam a aplicar a teoria de Fourier a soluções para as equações diferenciais parciais lineares mais simples, então estudou os espaços de Banach e Hilbert, bem como espaços de funções generalizadas, que é essencialmente a linguagem da mecânica quântica.

p Em meados do século 20, Espaços de Sobolev foram descobertos; estes agora ocupam uma das posições centrais na teoria das equações diferenciais parciais. Nos próximos 50 anos, eles ajudaram os matemáticos a encontrar muitas soluções para problemas aplicados que não podem ser encontrados em espaços funcionais comuns.

p Mais perto do início do século 21, tornou-se necessário encontrar novos métodos para estudar equações diferenciais parciais não lineares, assim, a matemática computacional e a teoria dos sistemas integráveis ​​foram desenvolvidas. Contudo, métodos desses campos acabaram sendo focados muito estreitamente, e a necessidade de desenvolver a linguagem ainda existe.

p Os espaços Lebesgue com normas mistas às vezes são objetos mais universais e flexíveis. Esses espaços são determinados da seguinte forma:No espaço de funções em várias variáveis, definir a norma iterando a norma de Lebesgue. Eles surgiram inicialmente como uma das generalizações dos espaços de Sobolev e já atraíram muito interesse de teóricos de vários países da Europa, assim como a China, Canadá e Rússia.

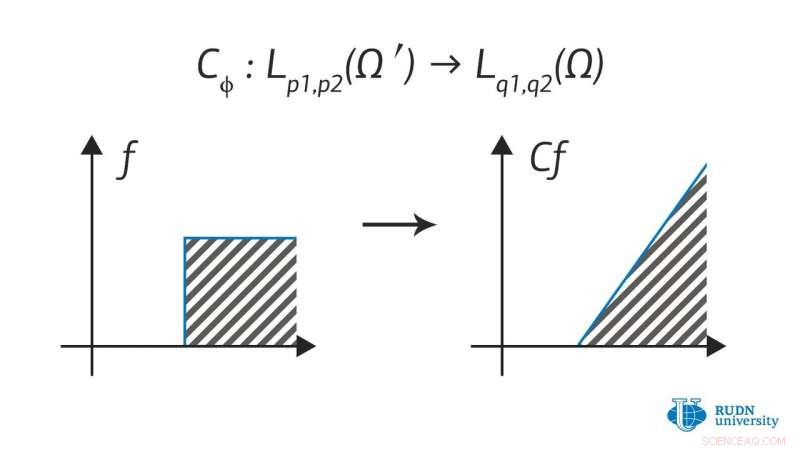
p Nikita Evseev e Alexander Menovshchikov do Instituto de Matemática da Universidade RUDN trabalham em uma teoria de operadores para tais espaços, o que permite seu uso em problemas aplicados formulados na linguagem de equações diferenciais parciais. Eles produziram uma série de novos resultados que descrevem as propriedades dos operadores em tais espaços:critérios para delimitação de operadores, propriedades de operadores integrais, operadores de multiplicação, operadores de composição, e muitos outros. Eles também obtiveram alguns resultados auxiliares úteis para o desenvolvimento posterior deste campo.

p "Nossos métodos e resultados, nós acreditamos, pode ser aplicado a problemas evolutivos e problemas diferenciais em regiões não cilíndricas. Por exemplo, em biologia (matemática), onde a superfície ou a área em estudo muda com o tempo, ou em hidrodinâmica, para problemas com um limite variável, "diz Evseev.

p A pesquisa neste campo é útil para estudar as equações de Navier-Stokes, um sistema de equações que descreve a aero- e hidrodinâmica. Os espaços Lebesgue com normas mistas permitem avaliar soluções, que, por sua vez, permite prever a ausência de turbulência, por exemplo.

p Os resultados também auxiliarão no estudo dos problemas aplicados da física matemática surgidos no estudo de materiais porosos e com trincas. Por exemplo, será possível prever teoricamente o padrão de difusão e transferência de calor em géis de sílica, vidros porosos, várias esponjas, e espumas, bem como em alguns materiais de construção.