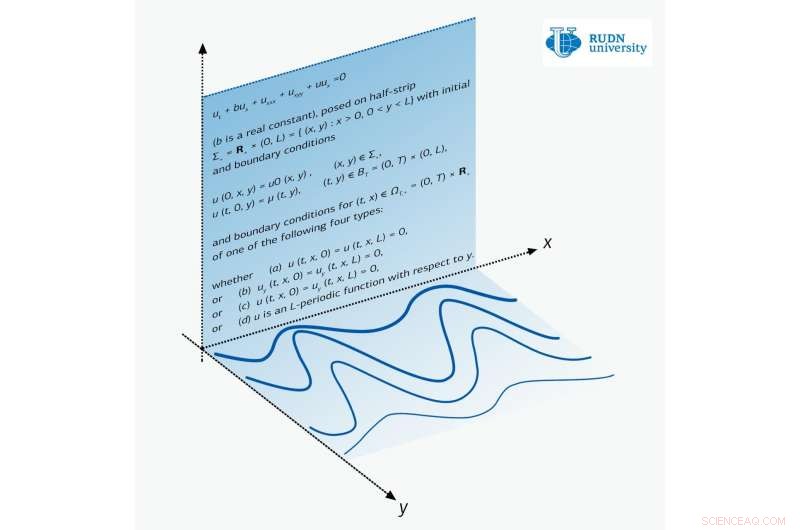
p Um matemático da Universidade RUDN provou pela primeira vez o teorema da existência e unicidade das soluções da equação de Zakharov-Kuznetsov em uma faixa. Esses teoremas são muito raros para equações diferenciais parciais. Os novos resultados podem ser aplicados em áreas como astrofísica, por exemplo, na descrição da propagação de ondas planas no plasma. O artigo está publicado na revista Análise não linear:aplicativos do mundo real . p A equação de Zakharov-Kuznetsov é uma equação de uma função de duas variáveis ​​x e y. Para a física, x é a direção da propagação da onda, e a deformação do meio ocorre ao longo da direção perpendicular y. Por exemplo, na oscilação de uma corda de violão, a onda parece correr pela corda, enquanto as oscilações ocorrem perpendicularmente em relação ao curso da onda.

p Há um grande número de resultados que descrevem soluções das equações de Zakharov-Kuznetsov no caso em que não há restrições em y. Mas a questão da propagação das ondas na faixa - quando y é limitado - não foi extensivamente estudada até recentemente.

p Os matemáticos da Universidade RUDN lidaram com a equação de Zakharov-Kuznetsov na faixa. Eles examinaram três casos principais - quando não há oscilações no limite da faixa, quando não há corrente no mesmo limite, e quando as condições de contorno são periódicas na estrutura. O último caso corresponde à propagação de ondas em um meio cuja estrutura é periódica em x.

p Em todos esses casos, os matemáticos conseguiram provar teoremas de existência e a singularidade de suas soluções. Para sistemas de equações diferenciais parciais, que incluem a equação de Zakharov-Kuznetsov, tais equações são muito raras.

p Esses resultados são os primeiros para soluções da equação com condições iniciais na faixa. Fluxos de plasma planos com condições de contorno, que estavam entre os fenômenos considerados pelos cientistas da Universidade RUDN, pode ocorrer na física e na astrofísica.

p As equações de Zakharov-Kuznetsov pertencem a uma categoria mais ampla de equações conhecida como equações de Korteweg-de Vries. No estudo desta categoria de equações, agora é possível descrever solitons - ondas cuja forma não muda durante o movimento. Os físicos consideram os solitons uma ferramenta para os modernos sistemas ópticos de transmissão de dados. O estudo dos solitons, que pode surgir nas equações de Zakharov-Kuznetsov, é uma das opções para o desenvolvimento do trabalho dos matemáticos da RUDN University.