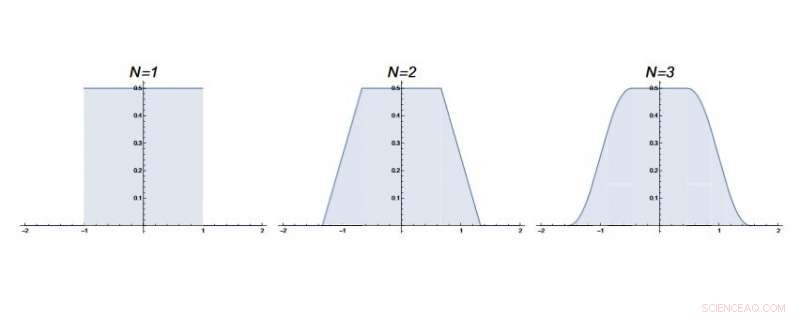
 p A "erosão" da densidade de probabilidade de caminhantes aleatórios na origem no oitavo passo de tempo (N ≥ 8, não mostrado) oferece alguma intuição física sobre por que um padrão encontrado em algumas integrais de Borwein quebra repentinamente no mesmo ponto. Crédito:Majumdar e Trizac. © 2019 American Physical Society
p A "erosão" da densidade de probabilidade de caminhantes aleatórios na origem no oitavo passo de tempo (N ≥ 8, não mostrado) oferece alguma intuição física sobre por que um padrão encontrado em algumas integrais de Borwein quebra repentinamente no mesmo ponto. Crédito:Majumdar e Trizac. © 2019 American Physical Society
p Os padrões aparecem amplamente na natureza e na matemática, das espirais de Fibonacci das conchas do mar à periodicidade dos cristais. Mas certos problemas matemáticos às vezes podem levar o solucionador humano a ver um padrão, mas então, fora do azul, o padrão desaparece repentinamente. Esses padrões ilusórios surgem em muitas áreas da matemática, com um exemplo vindo de certas integrais de cálculo que enganaram a intuição até mesmo dos melhores matemáticos. p Agora em um novo estudo, dois físicos abordaram essas integrais usando o conceito físico de passeios aleatórios. Considerando que resolver essas integrais geralmente requer um grande esforço e engenhosidade, os físicos mostraram que a nova abordagem pode encontrar soluções intuitivamente e às vezes até mesmo sem a necessidade de cálculos explícitos.
p Os físicos Satya N. Majumdar e Emmanuel Trizac da Universidade de Paris-Sud, CNRS, na França, publicaram um artigo sobre o uso de caminhantes aleatórios para resolver integrais em uma edição recente da
Cartas de revisão física.
p "Nós mostramos que o insight da física nos permite obter de uma forma livre de cálculos uma riqueza de integrais curiosas, e, além disso, para obter identidades previamente desconhecidas (integrais, ou igualdades entre somas discretas e integrais), "Trizac disse
Phys.org . "Nosso trabalho revela que quando a intuição matemática é enganada, a intuição física pode salvar o dia. "
p
Padrões em integrais de Borwein
p As integrais em questão (ver figura) são "integrais de Borwein, "com o nome de David e Jonathan Borwein (pai e filho), que notou padrões incomuns neles em 2001. As integrais de Borwein envolvem o produto de funções sinc (seno cardinal), que têm aplicações generalizadas, como na ótica, processamento de sinal, e outras áreas. Essas duas integrais particulares podem ser usadas para calcular os volumes dos hipercubos.
p Resolver os integrais de Borwein envolve a substituição de números pela variável
n . Cada número fornece um valor de solução diferente, permitindo que os matemáticos observem padrões na sequência de valores resultante. Por exemplo, para a primeira integral (I
n ), quando você substitui os números
n =1-7, você sempre obtém a resposta π. Mas quando você chegar a
n =8, a resposta é ligeiramente menor que π (aproximadamente π - 10
-10
) A primeira vez que os matemáticos calcularam este valor em um computador, eles pensaram que deve haver um bug no software. Mas a resposta foi confirmada, e os termos subsequentes (para
n =9, 10, etc.) ficam cada vez menores.
 p Crédito:Majumdar e Trizac. © 2019 American Physical Society
p Crédito:Majumdar e Trizac. © 2019 American Physical Society
p Alguns padrões persistem ainda mais. Para a segunda integral, J
n , os primeiros 56 termos da sequência (obtidos substituindo os números de 1 a 56 por
n ) são todos π / 2. Mas o 57
º
o termo é aproximadamente π / 2—10
-110
, e os mandatos subsequentes continuam diminuindo. (As coisas podem se tornar ainda mais extremas:para uma variante das integrais de Borwein - não discutidas aqui - um padrão de valor constante vale para um surpreendente primeiro 10
176
termos da sequência, depois disso, o padrão finalmente é quebrado.)
p Os matemáticos podem explicar por que esses padrões quebram repentinamente, pelo menos em termos matemáticos. Observe que ambas as integrais de Borwein acima contêm a função sinc (a
n k), onde um
n =1 / (2n — 1). Se você substituir nos números 1, 2, 3, … para
n nesta expressão, você obtém a sequência 1, 1/3, 1/5, 1/7, 1/9, ... Os Borweins notaram que o primeiro mandato, 1, não é apenas maior do que todos os outros termos que vêm depois, mas é ainda maior do que a soma dos próximos termos - do segundo ao sétimo termos, para ser exato, como 1/3 + 1/5 + 1/7 + 1/9 + 1/11 + 1/13 =0,955 ..., que é menor que 1. Mas ao adicionar o oitavo termo, 15/01, a esta soma, a resposta é 1,02 ..., logo acima de 1. Acontece que não é coincidência que o sétimo termo é o último termo para o qual a integral é avaliada como π, e o oitavo termo é o ponto em que o padrão é interrompido.
p Os Borweins provaram um teorema (veja a figura) que afirma essa ideia em termos mais gerais. O teorema é válido para a segunda integral, J
n , também. Contabilizando a função cosseno em J
n muda a expressão acima para 2 / (2n — 1), devido à propriedade cos (a) sinc (a) =sinc (2a), de modo que o primeiro termo é 2 em vez de 1. Como a soma do segundo até 56
º
termos da expressão é menor que 2, mas adicionando os 57
º
termo empurra a soma para 2, o teorema é válido.
p
Caminhantes aleatórios
p Embora o teorema ajude a explicar quando os padrões temporários das integrais de Borwein se quebram, ainda não está completamente claro por que o teorema é válido em primeiro lugar.
p No novo jornal, Majumdar e Trizac ofereceram alguma intuição física sobre o teorema, conectando-o a alguns conceitos bem compreendidos na teoria da probabilidade e na mecânica estatística. Eles notaram que a integral no teorema tem laços estreitos com a distribuição uniforme de probabilidade, que é amplamente utilizado em toda a ciência. Especificamente, a transformada de Fourier da distribuição de probabilidade uniforme passa a ser apenas a função sinc, que produz a integral de Borwein para
n =1. Esta conexão liga as integrais de Borwein ao mundo físico, de modo que, usando parâmetros relevantes, eventos que seguem uma distribuição uniforme podem ser usados para modelar a sequência de soluções para as integrais de Borwein.
p Para descrever esta conexão em um contexto mais físico, os pesquisadores observaram caminhantes aleatórios. Um caminhante aleatório é um objeto abstrato que pode se mover a uma certa distância em qualquer direção, onde a distância exata é escolhida aleatoriamente a partir de um intervalo contínuo de valores, e cada um desses valores tem a mesma probabilidade de ser escolhido (ou seja, segue uma distribuição uniforme). Caminhantes aleatórios podem modelar com precisão uma variedade de fenômenos aleatórios, como os preços do mercado de ações, os caminhos dos animais forrageiros, e os caminhos das moléculas em um gás, que ocorrem em um, dois, ou três dimensões, respectivamente.
p No novo jornal, the physicists show that the movements of infinitely many random walkers can be used to model the emergence and disappearance of the patterns in the Borwein integrals. To begin, the random walkers all start at the point zero on the one-dimensional number line. For the first step, each walker is allowed to move a random distance of up to 1 unit, either left or right. For the second step, each walker may move a random distance of up to 1/3, then a random distance of up to 1/5, then 1/7, 1/9, etc. That is, each successive allowable step distance corresponds to the next value of the expression 1/(2n—1).
p The main question is, what is the fraction of random walkers at the starting point (the origin) after each time step? It turns out that the fraction (more precisely, the probability density) of walkers at the origin at each time step
n corresponds to the solution to the Borwein integral using the same
n valor.
p As the physicists explain, for the first seven steps, the probability density that a walker ends up at the origin is always ½, which via the theorem above corresponds to an integral value of π. The key idea is that, up to this time, the density of walkers at the origin is the same as if the entire number line was uniformly populated with walkers. Na realidade, as the maximum distance of each step is restricted, only part of the number line is accessible, ou seja, the walkers' world is finite.
p Contudo, for the first seven steps, the walkers at the origin perceive that their world is infinite, since they do not possess any information about the existence of boundaries that would indicate that the world is finite. This is because none of those walkers that reached the outer boundary of their world (+1 or -1 after the first step) would have been able to make it back to the starting point in less than seven steps, even if taking the maximum size steps allowed and all in the direction toward the starting point. As these walkers had zero probability of showing up at the starting point before the eighth step, they could not affect the fraction of random walkers at the starting point. So for the first seven steps, the density of walkers at the origin is fixed at ½ (it is "protected").
p But once those walkers that have reached +1 or -1 return to the origin, the situation changes. After the eighth step, it's possible that some of these walkers return to the starting point. Now these walkers act as "messengers" in the sense that their return to the starting point reveals the existence of a boundary, telling the other walkers at the origin that their world is finite, and therefore influencing the density of walkers at the origin.
p Since these messenger walkers made it back to the starting point, it becomes clear that some other boundary-reaching walkers did not make it back, but instead may have kept continuing to move further away. Como resultado, the probability distribution becomes more spread out, causing the fraction of walkers at the origin to gradually erode from ½ (or π for the integral). It is this erosion that explains why the values of the first Borwein integral decrease ever so slightly for n ≥ 8. A similar argument holds for the second Borwein integral (see video).
p By connecting the Borwein integrals to the probabilities of random walkers, the new results offer a completely different approach to solving these integrals than through direct calculation. The physicists showed that the same approach can be applied to many other integrals in addition to the two described here, including extensions to higher dimensions. The researchers expect that the approach has the potential to provide calculation-free solutions to many other integrals that are otherwise very difficult to solve.
p "Random walk problems and their infinite ramifications form one of the cornerstones of modern physics with a wide range of applications in physics, chemistry, biologia, Engenharia, etc, " Trizac said. "Since our derivation of intriguing integrals involves basic concepts from random walk theory, we expect that new identities and integrals, with real-world applications, may be derived using our key idea in the near future." p © 2019 Science X Network

