p Um matemático RUDN desenvolveu uma solução para uma contenção diferencial perturbada - um caso generalizado de uma equação diferencial. O desenvolvimento calculará os caminhos ideais para o movimento de uma multidão ou fluxo de carros. Também pode ser usado para gerenciar carros robóticos e sistemas robóticos multiagentes. Os resultados do estudo foram publicados no Journal of Differential Equations . p A maioria dos processos físicos pode ser descrita por meio de equações diferenciais. Para fazer isso, uma quantidade desconhecida (por exemplo, temperatura ou velocidade) é apresentada como uma função. Uma equação diferencial pode ser escrita para tal função, e sua solução descreverá o comportamento da quantidade desconhecida. Contudo, em alguns casos, escrever uma equação diferencial é impossível, e os matemáticos têm de usar as chamadas contenções diferenciais - equações em que o sinal de igual é substituído pelo sinal de contenção ou inclusão. Um matemático RUDN desenvolveu uma solução abrangente para um grupo de contenções diferenciais e mostrou suas possíveis aplicações em casos de gestão de cidades.

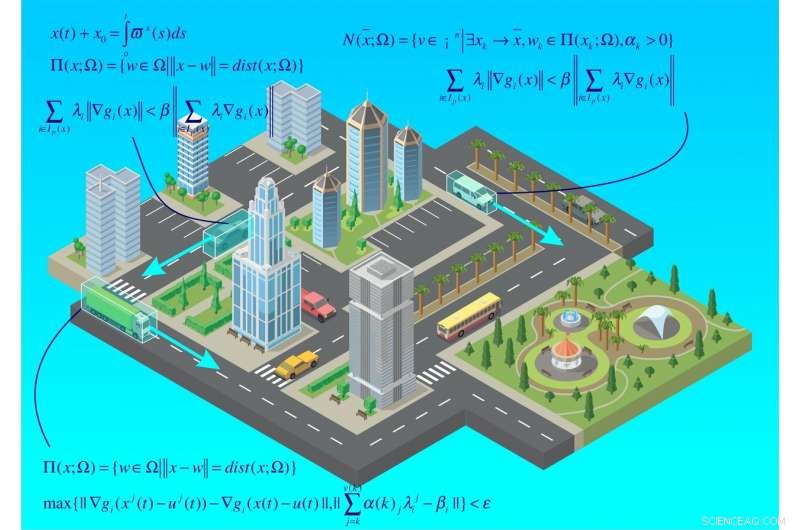
p Problemas de controle ótimo são cobertos por uma teoria especial em matemática. A ideia de tais problemas reside no desenvolvimento (quantitativa ou teoricamente) de uma lei de controle que levaria um sistema a um determinado estado da maneira mais eficiente. Imagine um carro que se aproxima do semáforo. Quando a distância entre eles é de 250 metros, a luz fica verde e permanece por 30 segundos. O problema de controle é calcular como o carro deve se mover para reduzir ao mínimo o consumo de energia. Inicialmente, isso pode parecer simples, mas observe que a aceleração e a desaceleração consomem o combustível. Portanto, tal problema está no escopo da teoria de controle ótimo e pode ser resolvido usando uma contenção diferencial.

p "Além do interesse teórico puro, a motivação para este estudo foi uma tarefa complicada que exigia controle ideal com limitações internas. Na prática, pode ser expresso como a descrição de uma multidão em um avião, "disse Boris Mordukhovich, um co-autor do trabalho, e um associado do Nikolsky Institute of Mathematics, RUDN.

p A contenção diferencial em questão pode descrever o movimento de uma multidão. Imagine que há muitas pessoas em uma sala, e cada um deles precisa sair o mais rápido possível. Contudo, só há uma saída. Os resultados obtidos pelos matemáticos irão calcular a trajetória e a velocidade de movimento de cada pessoa em particular.

p Os resultados do estudo podem ser aplicados na prática ao cálculo de rotas ótimas para carros robóticos. Outra área de aplicação possível são os sistemas robóticos multiagentes, ou seja, sistemas de vários robôs de IA trabalhando na mesma tarefa, como triagem ou transporte de mercadorias. Vários robôs deste tipo formam uma multidão, e para que seu trabalho seja eficiente, velocidades e trajetórias ideais devem ser calculadas para cada um deles.