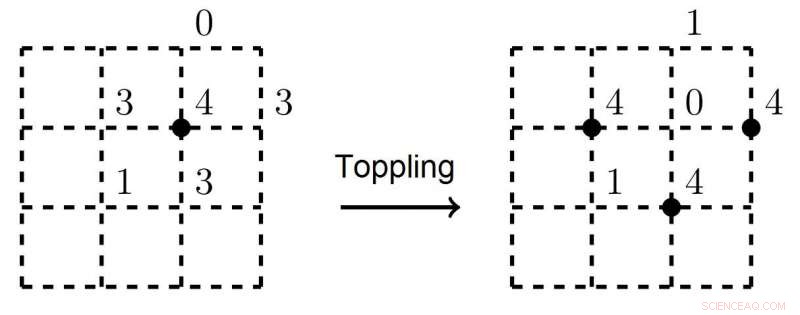
 p O ponto preto na figura à esquerda marca um vértice instável. Depois de uma avalanche, três vértices vizinhos tornam-se instáveis e entram em colapso. Crédito:Nikita Kalinin, Escola Superior de Economia - São Petersburgo
p O ponto preto na figura à esquerda marca um vértice instável. Depois de uma avalanche, três vértices vizinhos tornam-se instáveis e entram em colapso. Crédito:Nikita Kalinin, Escola Superior de Economia - São Petersburgo
p Um grupo internacional de pesquisadores (o primeiro autor é Nikita Kalinin, Escola Superior de Economia - São Petersburgo, o último autor é Ernesto Lupercio, CINVESTAV, México) apresentou o primeiro modelo contínuo que descreve a criticidade auto-organizada. A solução proposta é mais simples e universal do que o modelo clássico de pilha de areia. Integra áreas tão distantes umas das outras quanto a economia, biologia do desenvolvimento, e a gravidade no contexto da geometria tropical. O artigo foi publicado em
Proceedings of the National Academy of Sciences . p Diz-se que um sistema está em estado crítico se uma força externa, por menor que seja, pode produzir um efeito de avalanche, causando uma mudança no comportamento do sistema. Isso inclui as transições de fase:uma vez que um único cristal de gelo emerge na água resfriada a zero graus Celsius, um aglomerado de gelo começará a se formar imediatamente.
p Existem certos sistemas dinâmicos que tendem a um estado crítico - os terremotos são um exemplo ilustrativo. Embora uma certa temperatura e pressão sejam necessárias para que a água congele, nenhum parâmetro preciso precisa ser cumprido para que um terremoto aconteça. A principal causa dos terremotos é o movimento contínuo das placas tectônicas, e prever o momento exato em que o sistema atingirá um estado crítico e produzirá uma avalanche é virtualmente impossível.
p Muitos pesquisadores tentaram resolver o mistério dos terremotos. Em meados do século 20, Os sismólogos americanos Gutenberg e Richter mostraram uma relação entre a magnitude e o número total de terremotos em qualquer região. Essa relação é descrita pela lei de potência expressa como uma linha reta em uma escala logarítmica dupla.
p Fenômenos que compartilham essa característica já foram encontrados na geofísica, cosmologia, economia, teoria da gestão de risco e outros campos. Todos eles podem ser descritos pela teoria da criticidade auto-organizada (SOC).
p O conceito de SOC foi introduzido por Per Bak, Chao Tang e Kurt Wiesenfeld em 1987. Em seu artigo seminal, eles apresentaram o exemplo arquetípico de um sistema SOC:o modelo Sandpile. Imagine uma grade quadrada com grãos de areia em cada um de seus vértices, em que novos grãos estão caindo na grade com uma certa frequência. Supõe-se que, se não houver mais do que três grãos de areia em cada vértice, o sistema permanecerá estável. Mas assim que um quarto grão de areia cai no topo de um vértice, ele tomba, e a areia desliza para baixo neste pico e é redistribuída para os vértices vizinhos. O tombamento continuará em avalanche até que o sistema volte ao equilíbrio. A principal descoberta dos físicos foi que o número de vértices que tombam (ou seja, o tamanho da região colapsada) satisfaz uma distribuição de lei de potência.
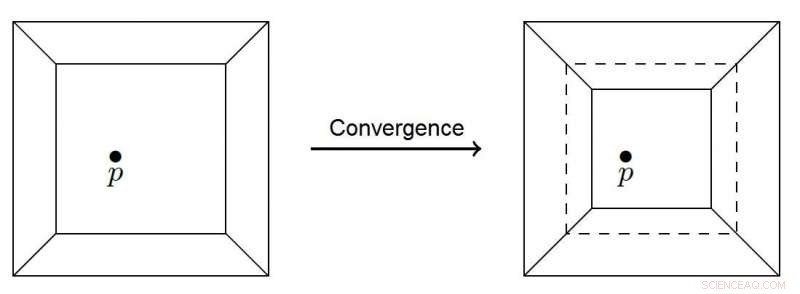 p Polígono convergindo para um ponto. Crédito:Nikita Kalinin, Escola Superior de Economia - São Petersburgo
p Polígono convergindo para um ponto. Crédito:Nikita Kalinin, Escola Superior de Economia - São Petersburgo
p O modelo de pilha de areia há muito é o modelo clássico que descreve o SOC. Contudo, ele descreve a dinâmica de sistemas críticos apenas no nível fenomenológico e não pode ser usado para simular um terremoto ou prever o comportamento de uma pilha de areia real.
p "O antigo modelo de pilha de areia, sendo puramente combinacional, está um pouco afastado do grande mundo da matemática. Nosso modelo é um passo à frente, porque tem todas as vantagens do modelo de pilha de areia, mas também é geométrico e contínuo, tornando muito mais fácil de usar, "explica a autora Nikita Kalinin, Pesquisador sênior do Laboratório Internacional de Teoria de Jogos e Tomada de Decisão de HSE. "Mostramos que as correlações de leis de potência podem ser obtidas em um sistema contínuo que não é um autômato celular com a ajuda da geometria tropical, que tem muitas aplicações hoje. "
p "A geometria tropical é um ramo da geometria do século XXI inspirado na geometria algébrica clássica que floresceu por causa de suas conexões com muitos campos da ciência, principalmente a teoria das cordas, "afirma o Dr. Ernesto Lupercio do CINVESTAV.
p Em vez da grade usada no modelo clássico de pilha de areia, o novo modelo de pilha de areia tropical considera uma curva tropical - um gráfico planar com arestas retilíneas - encerrada em um quadrado. A curva divide o quadrado em regiões poligonais, cada um contendo um conjunto de pontos escolhido aleatoriamente. Quando um novo ponto é adicionado, a curva tropical tenta passar por ele, e a região poligonal que contém a ponta é unida por meio de uma transferência paralela de suas bordas. Assim que uma das bordas atinge o ponto, o processo pára. Um novo ponto é então adicionado, e tudo começa de novo. O ponto anterior pode estar fora da curva novamente, e o sistema começará a se mover nessa direção.
p Este processo de convergência é uma variante finita da adição de grãos de areia a uma pilha de areia. No novo modelo, o tamanho da avalanche corresponde à área varrida pelas regiões convergentes no processo iniciado pela adição de um ponto aleatório. Os cientistas esperam que seu modelo ajude a esclarecer as relações entre os diferentes fenômenos que manifestam as propriedades do SOC.
p "Podemos observar semelhanças em diferentes fenômenos vistos pelas lentes da matemática. A geometria tropical tem aplicações na teoria das cordas, economia e biologia do desenvolvimento. O valor do nosso trabalho está em encontrar conexões em lugares inesperados. Isso significa que os métodos aplicados a uma área podem ser aplicados a outra. Você só precisa dar o próximo passo, "diz Kalinin.

