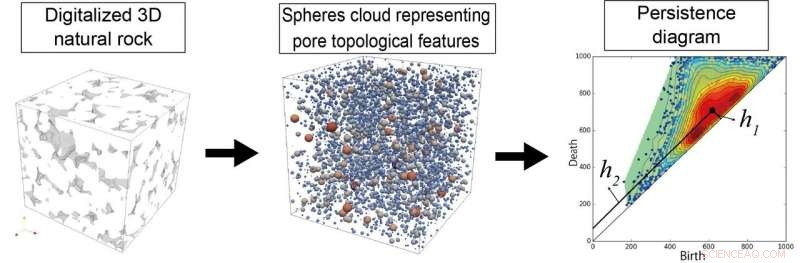
Figura:Esquerda:Esta é uma rocha natural 3D digitalizada, Centro:nuvem de esferas representando características topológicas de poros, À direita:Diagrama de persistência. Crédito:International Institute for Carbon Neutral Energy Research (I2CNER) / Institute of Mathematics for Industry (IMI), Universidade Kyushu
Com base na teoria da homologia persistente, pesquisadores da Universidade Kyushu do Japão apresentaram um novo parâmetro e um novo método para avaliar a heterogeneidade da porosidade
Fukuoka, Japão — Quer percebamos ou não, a matemática permeia nossas vidas de inúmeras maneiras. As vezes, o papel da matemática é difícil de entender, mas outras vezes é sólido como uma rocha.
Embora os grãos minerais que formam uma rocha sejam importantes, são os poros - os espaços vazios entre os grãos - que muitas vezes carregam recursos vitais, como petróleo, gás, e água potável. A geometria dos poros pode afetar fortemente o armazenamento, fluxo, e extração desses recursos. Assim, melhorar a compreensão da geometria dos poros é de grande interesse para muitos pesquisadores e profissionais da indústria.
Em uma fusão de matemática e ciências da terra, pesquisadores do Instituto Internacional de Pesquisa de Energia Neutra em Carbono (I2CNER) e do Instituto de Matemática para a Indústria (IMI) da Universidade de Kyushu desenvolveram agora um método inovador para caracterizar a geometria dos poros, com base em um conceito chamado teoria da homologia persistente, conforme relatado em um estudo publicado em Pesquisa de Recursos Hídricos .
Uma diferença importante entre rochas naturais e meios artificiais é que as características físicas das rochas tendem a ser relativamente heterogêneas. Este método de última geração é particularmente útil para caracterizar essa heterogeneidade em poros.
O primeiro autor do estudo, Fei Jiang, explica, “No método proposto, geometria de poro complexa é primeiro transformada em dados de nuvem de esfera. Então, um diagrama de persistência é calculado a partir da nuvem de pontos. Um novo parâmetro, o índice de distância H como uma métrica, é derivado do diagrama de persistência, e se propõe a caracterizar o grau de heterogeneidade das rochas. "
Uma forte relação foi confirmada entre a heterogeneidade e o índice de distância H. Além disso, uma nova equação empírica usando esta métrica H é proposta para prever o módulo de elasticidade efetivo das rochas.
"Para testar o novo método proposto com base na geometria de rochas reais, quatro tipos de rocha com diferentes estruturas de poros, incluindo dois carbonatos e dois arenitos, foram investigados, "O co-autor Takeshi Tsuji explica." A análise do diagrama de persistência foi mais eficaz para estimar quantitativamente a heterogeneidade de arenito relativamente homogêneo em comparação com o método convencional. Este novo método também foi superior em termos de distinguir os diferentes tipos de rochas. "
As vantagens adicionais deste método de análise são que o diagrama de persistência é relativamente estável, com pequenas mudanças no espaço dos poros, e o índice de distância H pode ser calculado de forma muito eficiente. As informações extraídas da análise do diagrama de persistência podem ser usadas para prever diretamente as propriedades físicas (como permeabilidade e elasticidade) com base nas microestruturas das rochas. Assim, A análise do diagrama de persistência pode revelar-se uma nova ferramenta importante para a compreensão da heterogeneidade dos poros em diferentes tipos de rocha.