p Se você já tentou desembaraçar um par de fones de ouvido, você entenderá como os laços e os cabos podem ficar torcidos. O DNA pode ficar emaranhado da mesma maneira, e em alguns casos, tem que ser cortado e reconectado para resolver os nós. Agora uma equipe de matemáticos, biólogos e cientistas da computação descobriram como a bactéria E. coli pode desvincular o DNA emaranhado por um processo de reconexão local. A matemática por trás da pesquisa, publicado recentemente em Relatórios Científicos , poderia ter implicações muito além da biologia. p A bactéria E. coli pode causar doenças intestinais, mas também são burros de carga de laboratório. O genoma de E. coli é um único círculo de DNA de fita dupla. Antes de uma célula de E. coli se dividir, esse círculo é copiado. Abrir a dupla hélice para copiá-la lança cepas de torção em outros lugares da molécula - da mesma forma que desenrolar um cordão em um lugar fará com que ele se enrole em outro lugar. O processo resulta em dois laços torcidos de DNA que passam um através do outro como um truque de "anéis mágicos".

p Para separar os anéis, E. coli usa uma enzima chamada topoisomerase IV, que corta precisamente um segmento de DNA, permite que os loops passem pelo intervalo e, em seguida, feche novamente o intervalo. Como a topoisomerase IV é tão importante para as bactérias, é um alvo tentador para antibióticos como a ciprofloxacina. Mas quando a topoisomerase IV está ausente, outro complexo enzimático pode intervir para realizar esta desvinculação, embora com menos eficiência. Este complexo introduz duas quebras e desvinculações ao reconectar as quatro pontas soltas.

p "Existem outras maneiras de desvincular os anéis, mas como eles fazem isso? "disse Mariel Vazquez, professor de matemática e de microbiologia e genética molecular na Universidade da Califórnia, Davis.

p Um caminho, Vazquez disse, é que as enzimas de reconexão removem um link de cada vez até chegarem a zero. Essa solução foi defendida pelos biólogos.

p Mas os matemáticos vêem o problema de maneira um pouco diferente. Eles entendem o DNA como uma curva flexível no espaço tridimensional. Certos pontos na curva podem ser quebrados e reconectados. Para um matemático, há muitas rotas possíveis para os processos de reconexão funcionarem - incluindo algumas nas quais o número de links realmente aumenta antes de diminuir.

p "Tudo isso é igual para um matemático, mas não para um biólogo, "Disse Vazquez. Para determinar a rota mais provável e resolver o problema, eles se voltaram para a modelagem computacional.

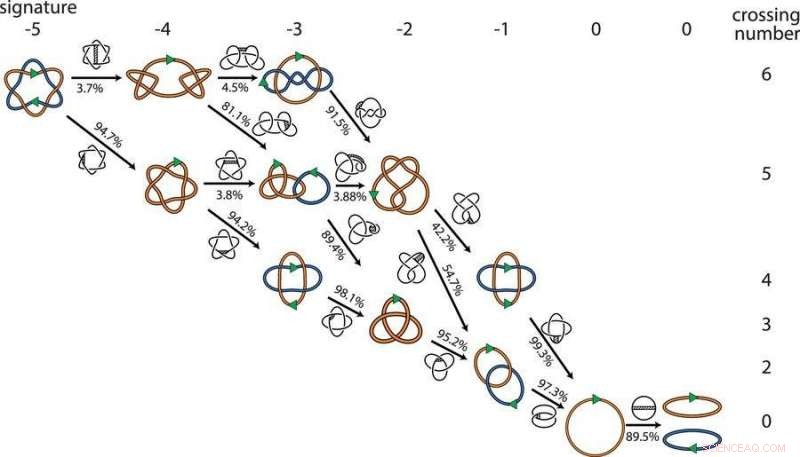
p Vazquez e seus colegas desenvolveram um software de computador com DNA representado como cadeias flexíveis para modelar os possíveis locais onde as enzimas de reconexão poderiam cortar e reconectar as cadeias. Geral, eles modelaram milhões de configurações que representam 881 topologias diferentes, ou formas matemáticas, e identificou centenas de caminhos mínimos para obter dois círculos de DNA ligados em até nove lugares em dois círculos separados.

p O modelo de computador confirmou o palpite dos biólogos:desfazer um link de cada vez é a rota preferida para separar os círculos do DNA.

p Os resultados podem ter implicações muito além da biologia do DNA, Vazquez disse. Existem outros exemplos na natureza de objetos que colidem, quebrar e reconectar - como a dinâmica de vórtices de fluidos ligados, ou os padrões formados por anéis de fumaça, por exemplo. Quando as erupções solares são ejetadas do sol, linhas de campo magnético poderosas se cruzam e se reconectam.

p "A matemática não é específica do DNA, e o cálculo pode ser adaptado, "Vazquez disse.