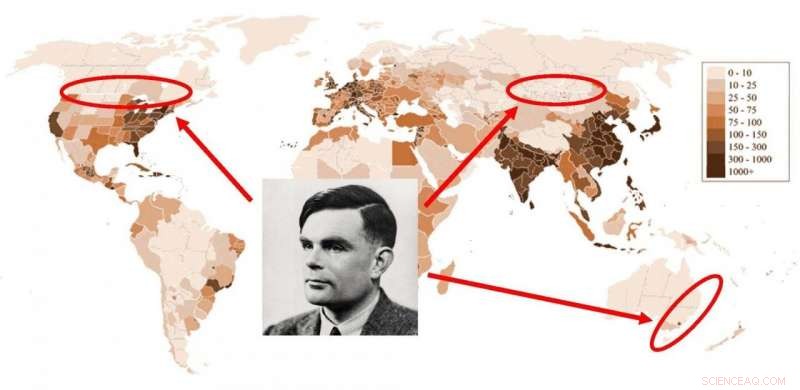
A teoria de formação de padrões de Alan Turing pode explicar a distribuição da população humana em todo o mundo. Crédito:Universidade de Leicester
O rápido crescimento da população humana global há muito é considerado um grande desafio que a humanidade enfrenta. Atualmente, este desafio está se tornando ainda mais sério do que antes, em particular porque estima-se que muitos recursos naturais se esgotem antes do final deste século.
Prevê-se que a crescente pressão populacional sobre a agricultura, os ecossistemas e o meio ambiente resultará na escassez mundial de alimentos e água, poluição, Falta de habitação, pobreza e tensão social. A situação é agravada pela mudança climática global, já que áreas consideráveis de terra serão inundadas e, portanto, retiradas do uso humano.
É amplamente aceito que, a menos que cenários alternativos de crescimento sustentável da população e desenvolvimento social sejam identificados e implementados, a humanidade provavelmente experimentará estagnação ou mesmo declínio.
O crescimento populacional no tempo é complementado com a dinâmica populacional no espaço. A distribuição da população no espaço é extremamente heterogênea por uma variedade de razões, para mencionar o clima, a história e a economia apenas como alguns. A heterogeneidade espacial pode resultar em fluxos migratórios significativos que, por sua vez, podem ter um feedback significativo sobre a demografia local e o crescimento populacional.
Em uma escala menor de países e estados individuais, a compreensão dos fatores que afetam a distribuição da população no espaço é necessária para garantir o desenvolvimento adequado da infraestrutura, rede de transporte e energia.
Decisões mal informadas podem resultar em superlotação e problemas sociais nas áreas urbanas e / ou menor qualidade de vida nos bairros rurais. A identificação de cenários de crescimento populacional sustentável e desenvolvimento social em várias escalas espaciais e temporais requer uma boa compreensão dos processos e mecanismos relevantes que afetam tanto o crescimento populacional quanto a distribuição populacional. Discutivelmente, é improvável que tal compreensão seja alcançada sem uma teoria bem desenvolvida e a estrutura matemática / de modelagem correspondente.
De fato, Os modelos matemáticos da dinâmica da população humana têm uma longa história que remonta ao século XVII. Nas últimas décadas, a necessidade de uma teoria matemática adequada e eficiente da dinâmica da população humana tem se refletido em um crescimento constante no número de estudos em que problemas de demografia, juntamente com questões relacionadas de economia, foram considerados usando modelos matemáticos. ferramentas e técnicas.
Em nosso artigo recente, usamos modelagem matemática para abordar o fenômeno da distribuição espacial heterogênea da população. Heterogeneidade de características geográficas (montanhas, florestas, rios, etc.) e recursos naturais (por exemplo, carvão, minério de ferro e cobre) são comumente aceitos como fatores que levam à heterogeneidade demográfica e econômica.
Aqui fazemos uma pergunta:esta heterogeneidade natural é a única causa subjacente, ou pode haver outro princípio, talvez mais geral, responsável pelo surgimento de distribuição populacional heterogênea? Para responder a esta pergunta, primeiro revisamos os dados disponíveis sobre a densidade populacional em algumas áreas em diferentes partes do mundo para mostrar que, em todos os casos considerados, a distribuição da população exibe um claro padrão espacial quase periódico, apesar do fato de que as condições ambientais são relativamente uniformes. Inspirado por esta descoberta, em seguida, consideramos um novo modelo de dinâmica econômico-demográfica acoplada no espaço e no tempo e nos esforçamos para usá-lo para simular a distribuição espacial da população. O modelo consiste em duas equações diferenciais parciais acopladas do tipo reação-difusão.
Seguindo uma abordagem de modelagem semelhante que foi usada com sucesso em ecologia e biologia, mostramos que o surgimento de padrões espaciais em nosso modelo parece ser possível como resultado da instabilidade de Turing.
Embora não seja nosso objetivo fornecer qualquer comparação direta entre os padrões demográficos do mundo real e as propriedades do modelo, consideramos a concordância qualitativa entre as previsões do modelo e os dados sobre a densidade da população humana como uma indicação de que a distribuição populacional heterogênea observada em diferentes países em diferentes continentes pode, pelo menos em alguns casos, foram causados por fatores endógenos em vez de fatores exógenos, ou seja, pode ter surgido devido à instabilidade de Turing intrínseca do sistema dinâmico econômico-demográfico correspondente.
Em muitos países, a distribuição da população no espaço é distintamente heterogênea, por exemplo. áreas urbanizadas com alta densidade populacional alternam-se com áreas rurais com baixa densidade populacional. Pelo visto, a variação espacial em fatores geográficos e climáticos pode desempenhar um papel significativo na formação da distribuição da população.
Nossa principal hipótese em nosso artigo é a existência de um mecanismo dinâmico que pode levar à formação de uma distribuição populacional heterogênea independente da heterogeneidade geográfica. Em nossa busca por exemplos do mundo real, nos concentramos nos casos em que o ambiente pode ser considerado, até uma certa escala espacial, como relativamente uniforme. As propriedades ambientais que consideramos aqui como proxies para a heterogeneidade ambiental são a elevação, a temperatura média anual e a precipitação média anual.