p Em 5 de janeiro, Rosa Winter obterá o doutorado em geometria aritmética. Ela pesquisou soluções de equações que definem as chamadas superfícies 'del Pezzo. "" Gosto da geometria porque posso imaginar e desenhar as formas e objetos, "diz Winter." Isso faz com que a matemática abstrata pareça mais tangível. " p Na matemática, às vezes é útil estudar equações abstratas usando objetos geométricos, como círculos, esferas, octaedra, ou mesmo objetos de dimensões superiores. O campo que conecta a geometria com equações abstratas é chamado de geometria aritmética. Ph.D. a candidata Rosa Winter aplicou esse tipo específico de geometria em sua tese.

p Superfícies de desenho

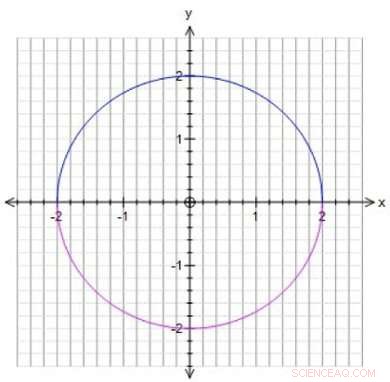
p Equações matemáticas podem definir objetos geométricos, o que significa que é possível estudar soluções para essas equações usando geometria. Por exemplo, se você quiser saber quais números você pode inserir para tornar x ^ 2 + y ^ 2 igual a 4, você pode desenhar todos os pontos (soluções) para os quais x ^ 2 + y ^ 2 =4. Isso resulta em um círculo com raio 2, que mostra, por exemplo, que o ponto x =2, y =0 é uma solução. Você também pode procurar soluções específicas, como pontos no círculo onde x e y são frações (1/3, 1/5, mas também, 0, 2, etc.). Essas soluções fracionárias são chamadas de pontos racionais. Winter estudou pontos racionais nas superfícies. "As superfícies são sempre bidimensionais, mesmo que vivam em oito dimensões, "diz Winter." O que significa que posso desenhar superfícies, tornando a matemática abstrata mais intuitiva para mim. "

p Pergunta de um milhão de dólares

p Encontrar pontos racionais em objetos geométricos raramente é fácil. Isso é mostrado, por exemplo, pela chamada "conjectura de Birch e Swinnerton-Dyer". Essa conjectura matemática ainda não comprovada faz parte dos Problemas do Prêmio do Milênio. O Clay Mathematics Institute concede um milhão de dólares para uma solução correta para qualquer um desses problemas. A conjectura é sobre pontos racionais em curvas elípticas. Como círculos, curvas elípticas são objetos geométricos definidos por certas equações. Quando você os desenha, eles se parecem com linhas curvas. Inverno:"Mesmo em curvas elípticas, sobre o qual sabemos um pouco, não é fácil determinar o conjunto de pontos racionais. "

p Superfícies Del Pezzo

p Infelizmente, Winter não arrecadou o milhão de dólares durante seu doutorado. pesquisar. Ela não trabalhou em pontos racionais em curvas elípticas, mas nas chamadas 'superfícies del Pezzo de grau 1. "Inverno:" De um ponto de vista geométrico, estes não são os mais difíceis, superfícies mais complicadas, mas eles ainda contêm questões matemáticas sem resposta. "Ela mostrou para parte desta família de superfícies que contém um número infinito de pontos racionais que não se agrupam; eles podem ser encontrados espalhados ao redor das superfícies. Se os pontos racionais fossem visíveis como pontos vermelhos e você poderia caminhar sobre uma superfície del-Pezzo, você veria pontos racionais vermelhos em todos os lugares que olhasse.

p Desde setembro, Winter trabalha como pós-doutorado no Instituto Max Planck de Matemática nas Ciências em Leipzig. Aqui ela aprende, entre outras coisas, como aplicar geometria e matemática abstrata em outras ciências, como biologia e física.