Como você prova algo? O que é mesmo a prova?

Em ciência, a palavra "prova" é usada raramente e com muito cuidado. Os cientistas aceitam que o mundo natural está cheio de surpresas, e o que parece ser verdade pode ter exceções.

Nos tribunais, a prova frequentemente inclui uma advertência, como "no equilíbrio das probabilidades" para questões civis, e "além de qualquer dúvida razoável" para casos criminais.

Mas para matemáticos como o Dr. Nick Beaton da Universidade de Melbourne, Professor Jan de Gier e Professor Tony Guttmann, "além da dúvida razoável" simplesmente não é bom o suficiente. Para eles, uma prova matemática está "além de qualquer dúvida" - e é algo belo.

Considere o teorema de Pitágoras.

Todos nós aprendemos na escola que o quadrado do lado mais comprido de um triângulo retângulo é a soma dos quadrados dos outros dois lados. Você pode testar isso com um pedaço de papel, uma régua e uma calculadora, e você verá que é verdade.

Você poderia fazer isso para mil triângulos e verá que é verdade para cada um desses mil triângulos.

Mas o Teorema de Pitágoras funciona para todos os triângulos retângulos possíveis?

Você não pode medir cada triângulo retângulo que existe, portanto, o método da régua e da calculadora não pode provar definitivamente que Pitágoras estava certo.

"Você faz muitas simulações e observa uma certa coisa numericamente, e se você observar isso repetidamente, pensaria que provavelmente é sempre assim, ou é verdade, "diz o Dr. Nick Beaton.

"Mas isso não é exatamente o mesmo que ter uma prova matemática onde você pode realmente mostrar logicamente que certa coisa sempre acontece em certos valores dos parâmetros."

Sem uma prova matemática formal, chamamos algo como o teorema de Pitágoras de conjectura.

O professor De Gier diz que uma conjectura em matemática é um resultado que todos acreditam ser verdade.

"Mas não foi provado logicamente em um sentido rigoroso, " ele diz.

"Então, pode haver muitas evidências numéricas e pode haver argumentos fortes e convincentes, mas eles não estão estabelecendo uma verdade além da dúvida.

"Um ótimo exemplo é a hipótese de Riemann sobre os zeros da função zeta, que foi verificado nos primeiros 10, 000, 000, 000, 000 (dez trilhões) de casos. Uma prova de que é verdade para todos os casos ainda está faltando e vale um milhão de dólares, "diz o professor De Gier.

"Prová-lo lançaria luz sobre muitos dos mistérios que cercam a distribuição dos números primos."

"E, ocasionalmente, algo parece muito convincente, mas depois é mostrado, uma vez que você se aprofunda nos mínimos detalhes, que ele realmente não se sustenta e pode haver exceções. "

A Wikipedia ainda tem uma categoria para "Conjecturas Reprovadas" - alguns, como a conjectura de Euler, permaneceu por centenas de anos antes de ser refutada.

No caso do Teorema de Pitágoras, Contudo, a prova está conosco há milhares de anos. Na verdade, Pitágoras não inventou a fórmula, era conhecido muito antes de seu tempo. Ele apresentou a primeira prova conhecida.

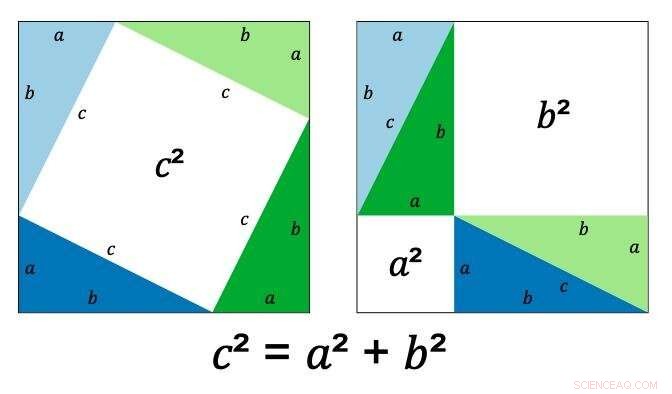
A prova de Pitágoras usa o fato indiscutível de que qualquer triângulo retângulo pode ser representado por dois quadrados, um dentro do outro, com os cantos do quadrado interno tocando a borda do externo.

O quadrado interno tem lados de comprimento c (o comprimento real não importa porque c pode ser qualquer número positivo), o quadrado externo tem comprimento a + b, e o triângulo que ele faz tem comprimentos laterais a, bec (como mostrado).

Alterar o ângulo do quadrado interno altera os comprimentos de todos os três valores.

Pitágoras mostrou que, reorganizando os triângulos dentro do quadrado, a área branca, representado por c² no diagrama acima, torna-se dois quadrados, um com área a² e outro com área b². Portanto, c² é sempre, não importa quais dimensões você usa, igual a a² + b².

Desde Pitágoras, os matemáticos ao longo dos tempos continuaram a encontrar provas do teorema. Em 1940, O matemático americano Elisha Scott Loomis publicou uma coleção de provas do Teorema de Pitágoras.

A equipe da Universidade de Melbourne conhece bem as provas.

A Australian Mathematical Society concedeu ao Dr. Beaton o Prêmio Gavin Brown 2018 de melhor artigo, Professor de Gier e Professor Guttman, junto com Mireille Bousquet-Mélou da Université de Bordeaux na França e Hugo Duminil-Copin da Université de Genève na Suíça, para uma prova matemática de 2015 da existência e tensão superficial crítica para adsorção de polímeros (moléculas de cadeia longa) em solução.

A equipe usou uma representação matemática de um polímero, chamado de "caminhada evasiva, "que são objetos usados ​​em um ramo da física matemática chamado de mecânica estatística.

"Uma caminhada evasiva é uma caminhada em uma treliça - muitas vezes uma treliça quadrada ou uma treliça de favo de mel - onde você não pode refazer nenhum dos passos que deu, "Professor Guttmann diz.

"Você pode pensar em uma caminhada como um único polímero, com propriedades aleatórias. "

Dr. Beaton diz que, muitas vezes, encontrar uma prova matemática para uma conjectura é uma longa, processo difícil, envolvendo tentativa e erro, trabalho pesado e ocasionais momentos de eureca.

Para Pitágoras, o momento eureka era a representação quadrado em quadrado do triângulo; para a equipe de Melbourne e seus colegas, era encontrar a melhor maneira de lidar matematicamente com a aleatoriedade.

"As pessoas tentaram algumas coisas quando foi conjeturado pela primeira vez, mas ninguém fez muito progresso, então ficou claro que uma nova ideia era necessária, mas o que essa nova ideia deveria ser não era óbvio, "diz o professor De Gier.

Depois de seguir alguns becos sem saída, a equipe se concentrou em uma nova ideia em matemática associada a modelos de rede, chamado de "holomorficidade discreta, "que foi popularizado pelo pesquisador russo Professor Stanislav Smirnov, que ganhou a Medalha Fields por descobertas notáveis ​​em matemática em 2010.

Usando este novo tipo de matemática, a equipe de Melbourne descobriu que a estrutura em favo de mel era o cenário certo para provar seu problema de polímero.

"Por algum motivo, a matemática da autoevitação anda em uma treliça de favo de mel funcionou muito bem, "Professor de Gier diz.

"Se você quiser fazer isso em uma rede quadrada, não funciona, mas para outros problemas, a estrutura quadrada seria melhor. "

O professor de Gier diz que uma prova matemática não é apenas um exercício intelectual, pode nos dizer coisas fundamentais sobre a natureza.

"Saber que algo acontece ou onde acontece é de interesse, mas ter esse raciocínio lógico é mais interessante porque dá uma ideia de por que as coisas acontecem da maneira que acontecem. "