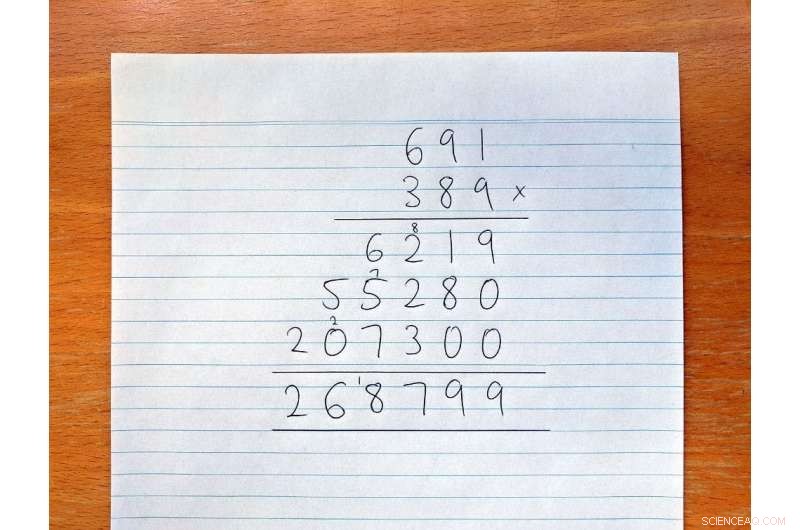p A multiplicação de dois números é fácil, direito? p Na escola primária, aprendemos como fazer multiplicações longas assim:

p Métodos semelhantes a este remontam a milhares de anos, pelo menos para os antigos sumérios e egípcios.

p Mas essa é realmente a melhor maneira de multiplicar dois grandes números juntos?

p Na multiplicação longa, temos que multiplicar cada dígito do primeiro número por cada dígito do segundo número. Se os dois números cada um tiver N dígitos, isso é N ² (ou N x N ) multiplicações completamente. No exemplo acima, N é 3, e tivemos que fazer 3 ² =9 multiplicações.

p Por volta de 1956, o famoso matemático soviético Andrey Kolmogorov conjecturou que este é o melhor maneira possível para multiplicar dois números juntos.

p Em outras palavras, não importa como você organiza seus cálculos, a quantidade de trabalho que você tem que fazer será proporcional a pelo menos N ² . O dobro de dígitos significa quatro vezes mais trabalho.

p Kolmogorov sentiu que se um atalho fosse possível, certamente já teria sido descoberto. Afinal, as pessoas multiplicam seus números há milhares de anos.

p Este é um excelente exemplo da falácia lógica conhecida como "o argumento da ignorância".

p Uma maneira mais rápida

p Apenas alguns anos depois, A conjectura de Kolmogorov mostrou-se espetacularmente errada.

p Em 1960, Anatoly Karatsuba, um estudante de matemática de 23 anos na Rússia, descobriu um truque algébrico que reduz o número de multiplicações necessárias.

p Por exemplo, para multiplicar números de quatro dígitos, em vez de precisar de 4 ² =16 multiplicações, O método de Karatsuba sai com apenas nove. Ao usar seu método, duas vezes mais dígitos significa apenas três vezes mais trabalho.

p Isso acumula uma vantagem impressionante à medida que os números aumentam. Para números com mil dígitos, O método de Karatsuba precisa de cerca de 17 vezes menos multiplicações do que a multiplicação longa.

p Mas por que diabos alguém iria querer multiplicar tantos números juntos?

p Na verdade, há um grande número de aplicativos. Uma das mais visíveis e economicamente significativas está na criptografia.

p Grandes números na vida real

p Sempre que você se envolver em uma comunicação criptografada na Internet, por exemplo, acesse o site do seu banco ou faça uma pesquisa na web - o seu dispositivo realiza um grande número de multiplicações, envolvendo números com centenas ou mesmo milhares de dígitos.

p É muito provável que seu dispositivo use o truque de Karatsuba para essa aritmética. Tudo isso faz parte do incrível ecossistema de software que mantém nossas páginas da web carregando o mais rápido possível.

p Para algumas aplicações mais esotéricas, matemáticos têm que lidar com números ainda maiores, com milhões, bilhões ou mesmo trilhões de dígitos. Para números tão enormes, até mesmo o algoritmo de Karatsuba é muito lento.

p Um verdadeiro avanço veio em 1971 com o trabalho dos matemáticos alemães Arnold Schönhage e Volker Strassen. Eles explicaram como usar a transformada rápida de Fourier (FFT) publicada recentemente para multiplicar números enormes com eficiência. Seu método é rotineiramente usado por matemáticos hoje para lidar com números na casa dos bilhões de dígitos.

p O FFT é um dos algoritmos mais importantes do século XX. Um aplicativo familiar na vida cotidiana é o áudio digital:sempre que você ouvir MP3s, serviços de streaming de música ou rádio digital, Os FFTs lidam com a decodificação de áudio nos bastidores.

p Uma maneira ainda mais rápida?

p Em seu artigo de 1971, Schönhage e Strassen também fizeram uma conjectura impressionante. Explicar, Terei que ser um pouco técnico por um momento.

p A primeira metade de sua conjectura é que deveria ser possível multiplicar N - números de dígitos usando um número de operações básicas que é proporcional a no máximo N registro ( N ) (isso é N vezes o logaritmo natural de N )

p Seu próprio algoritmo não atingiu esse alvo; eles eram muito lentos por um fator de log (log N ) (o logaritmo do logaritmo de N ) No entanto, sua intuição os levou a suspeitar que algo estava faltando, e essa N registro ( N ) deve ser viável.

p Nas décadas desde 1971, alguns pesquisadores encontraram melhorias no algoritmo de Schönhage e Strassen. Notavelmente, um algoritmo projetado por Martin Fürer em 2007 chegou agonizantemente perto do elusivo N registro ( N )

p A segunda (e muito mais difícil) parte de sua conjectura é que N registro ( N ) deve ser o limite de velocidade fundamental - nenhum algoritmo de multiplicação possível poderia fazer melhor do que isso.

p Soa familiar?

p Chegamos ao limite?

p Algumas semanas atrás, Joris van der Hoeven e eu postamos um artigo de pesquisa que descreve um novo algoritmo de multiplicação que finalmente atinge o N registro ( N ) cálice Sagrado, resolvendo assim a parte "fácil" da conjectura de Schönhage-Strassen.

p O artigo ainda não foi revisado por pares, portanto, algum cuidado é necessário. É prática padrão em matemática disseminar os resultados da pesquisa antes de serem submetidos à revisão por pares.

p Em vez de usar FFTs unidimensionais - o grampo de todos os trabalhos sobre este problema desde 1971 - nosso algoritmo depende de multidimensional FFTs. Esses gadgets não são novidade:o formato de imagem JPEG amplamente usado depende de FFTs bidimensionais, e FFTs tridimensionais têm muitas aplicações em física e engenharia.

p Em nosso jornal, usamos FFTs com 1, 729 dimensões. Isso é difícil de visualizar, mas matematicamente não mais problemático do que o caso bidimensional.

p Mesmo, números realmente grandes

p O novo algoritmo não é muito prático em sua forma atual, porque a prova fornecida em nosso artigo só funciona para números absurdamente grandes. Mesmo se cada dígito foi escrito em um átomo de hidrogênio, não haveria espaço suficiente disponível no universo observável para anotá-los.

p Por outro lado, temos esperança de que, com mais refinamentos, o algoritmo pode se tornar prático para números com apenas bilhões ou trilhões de dígitos. Se então, pode muito bem se tornar uma ferramenta indispensável no arsenal do matemático computacional.

p Se a conjectura Schönhage-Strassen completa estiver correta, então, de um ponto de vista teórico, o novo algoritmo é o fim da linha - não é possível fazer melhor.

p Pessoalmente, Eu ficaria muito surpreso se a conjectura estivesse errada. Mas não devemos esquecer o que aconteceu com Kolmogorov. A matemática às vezes pode trazer surpresas. p Este artigo foi republicado de The Conversation sob uma licença Creative Commons. Leia o artigo original.