p Os cientistas da RUDN criaram um modelo matemático que descreve as mudanças nas propriedades dos tecidos cerebrais após o derrame. O desenvolvimento ajudará os médicos a otimizar a terapia pós-AVC, estimulando os neurônios do cérebro e levando em consideração a situação individual de cada paciente. Os resultados do estudo foram publicados em Biociências Matemáticas . p Mais de 15 milhões de pessoas têm derrames todos os anos. Um derrame é uma falha aguda da circulação sanguínea no cérebro que mata as células neurais. Pacientes que sofrem um acidente vascular cerebral muitas vezes enfrentam perda parcial ou total da fala, e têm dificuldade para mover seus membros ou todo o corpo. Um método de reabilitação após um derrame é a estimulação do córtex cerebral com eletrodos implantados no cérebro ou impulsos magnéticos. O sucesso da terapia depende de muitos fatores, incluindo a área do cérebro que é estimulada e os tipos de sinais usados. Atualmente, os parâmetros de terapia ideais são selecionados manualmente. Os matemáticos RUDN criaram um modelo teórico para basear essa seleção em cálculos exatos.

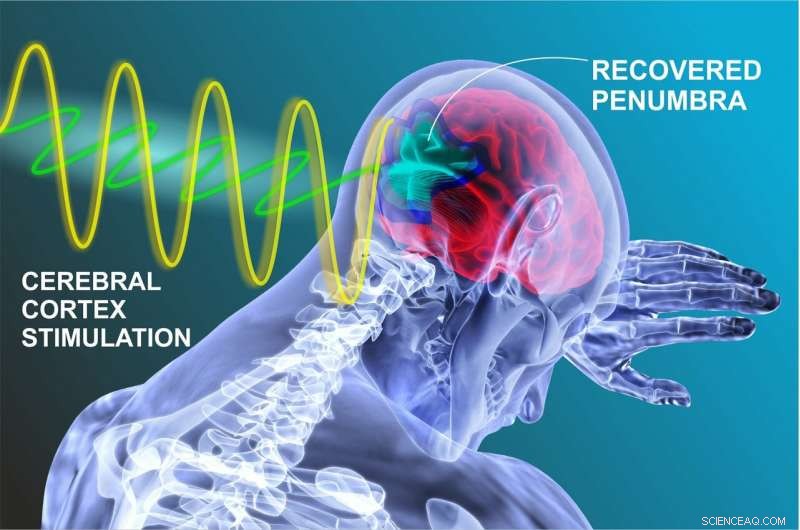
p "Nossa tarefa foi desenvolver um modelo teórico que descreve como a velocidade de propagação do impacto nervoso (ou seja, a excitação do tecido) diminui devido a danos pós-AVC no córtex cerebral. Além disso, demonstramos que, em certos casos, a estimulação elétrica do cérebro pode compensar esse processo, "disse Vitaly Volpert, o autor do artigo, e chefe do laboratório de modelagem matemática em biomedicina da RUDN.

p Depois de um derrame, uma chamada penumbra se forma no cérebro. É uma área onde o suprimento de sangue é reduzido em comparação com os requisitos para o funcionamento normal, mas que ainda é mais alto do que o nível crítico após o qual ocorre uma mudança irreversível. As células da penumbra se tornam menos excitáveis ​​e perdem a conexão com outros neurônios, levando a mudanças na forma e na velocidade da onda de excitação. Os matemáticos RUDN calcularam as condições nas quais a velocidade dos impulsos neurais pode ser restaurada aos níveis normais com a ajuda de estimulação externa.

p O modelo é baseado na teoria do tecido nervoso contínuo. A ideia é que o tecido do córtex cerebral seja apresentado como um fino, superfície plana. Essa suposição pode ser feita devido à alta densidade de neurônios (cerca de 100, 000 por 1 mm ² ) e a espessura do córtex, o que equivale a apenas 2,5 mm.

p Ao desenvolver o modelo, Os matemáticos RUDN introduziram a chamada função de conexão. Mostra que dois pontos na superfície do córtex cerebral estão conectados dependendo da distância entre eles. O potencial elétrico em cada ponto é expresso como uma função indeterminada dependendo do tempo e das coordenadas do ponto. Para esta função, os cientistas escreveram a principal equação diferencial integro do modelo. Seus principais parâmetros incluem o limiar de excitação dos neurônios (uma quantidade mínima de energia necessária para "irritar" um neurônio) e a amplitude da excitação. Quando um cérebro é estimulado eletricamente, esses dois parâmetros são afetados. Portanto, os médicos precisam descobrir como a solução muda com diferentes parâmetros de equação. Os autores estudaram a equação e deduziram várias condições (equações e inequações matemáticas). Quando eles são encontrados, a estimulação do córtex cerebral externo pode compensar totalmente as consequências de um acidente vascular cerebral.

p "O modelo sugerido é construído tendo em vista cálculos matemáticos recentes, tecnologias de ponta, e dados sobre propriedades cerebrais. Usando nosso desenvolvimento, os médicos podem adaptar a estimulação do córtex cerebral às necessidades de cada paciente, ou seja, tornar a terapia pós-AVC consistente com os padrões de medicina personalizada, "acrescentou Vitaly Volpert.