 p Manuscrito Bakhshali. Crédito:Bibliotecas Bodleian, Universidade de Oxford
p Manuscrito Bakhshali. Crédito:Bibliotecas Bodleian, Universidade de Oxford
p Não deve ser surpresa que o primeiro uso registrado do número zero, descoberto recentemente para ser feito já no século 3 ou 4, aconteceu na Índia. A matemática no subcontinente indiano tem uma rica história que remonta a 3, 000 anos e prosperou por séculos antes de avanços semelhantes serem feitos na Europa, com sua influência se espalhando para a China e o Oriente Médio. p Além de nos dar o conceito de zero, Matemáticos indianos fizeram contribuições seminais para o estudo da trigonometria, álgebra, números aritméticos e negativos, entre outras áreas. Talvez o mais significativo, o sistema decimal que ainda empregamos em todo o mundo foi visto pela primeira vez na Índia.
p
O sistema numérico
p Já em 1200 AC, o conhecimento matemático estava sendo escrito como parte de um grande corpo de conhecimento conhecido como Vedas. Nestes textos, os números eram comumente expressos como combinações de potências de dez. Por exemplo, 365 pode ser expresso como três centenas (3x10²), seis dezenas (6x10¹) e cinco unidades (5x10⁰), embora cada potência de dez fosse representada com um nome em vez de um conjunto de símbolos. É razoável acreditar que essa representação usando potências de dez desempenhou um papel crucial no desenvolvimento do sistema de valores de casas decimais na Índia.
p A partir do século III aC, também temos evidências escritas dos numerais Brahmi, os precursores do moderno, Sistema numeral indiano ou hindu-arábico que a maior parte do mundo usa hoje. Uma vez que o zero foi introduzido, quase toda a mecânica matemática estaria em vigor para permitir que os antigos indianos estudassem matemática superior.
p
O conceito de zero
p O próprio Zero tem uma história muito mais longa. Os primeiros zeros registrados recentemente datados, no que é conhecido como o manuscrito Bakhshali, eram simples marcadores de posição - uma ferramenta para distinguir 100 de 10. Marcas semelhantes já haviam sido vistas nas culturas babilônica e maia nos primeiros séculos dC e indiscutivelmente na matemática suméria já em 3000-2000 aC.
p Mas apenas na Índia o símbolo de espaço reservado para nada progrediu para se tornar um número por direito próprio. O advento do conceito de zero permitiu que os números fossem escritos de forma eficiente e confiável. Por sua vez, isso permitiu a manutenção de registros eficazes, o que significava que cálculos financeiros importantes poderiam ser verificados retroativamente, garantindo as ações honestas de todos os envolvidos. Zero foi um passo significativo no caminho para a democratização da matemática.
p Essas ferramentas mecânicas acessíveis para trabalhar com conceitos matemáticos, em combinação com uma cultura acadêmica e científica forte e aberta, quis dizer isso, por volta de 600 DC, todos os ingredientes estavam prontos para uma explosão de descobertas matemáticas na Índia. Em comparação, esses tipos de ferramentas não foram popularizados no Ocidente até o início do século 13, embora o livro de Fibonnacci, liber abaci.
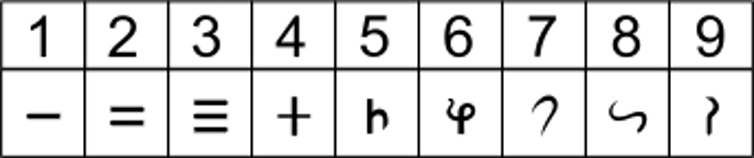 p Números Brahmi. Crédito:Wikimedia
p Números Brahmi. Crédito:Wikimedia
p
Soluções de equações quadráticas
p No sétimo século, as primeiras evidências escritas das regras para trabalhar com o zero foram formalizadas no Brahmasputha Siddhanta. Em seu texto seminal, o astrônomo Brahmagupta introduziu regras para resolver equações quadráticas (tão apreciadas pelos alunos de matemática do ensino médio) e para calcular raízes quadradas.
p
Regras para números negativos
p Brahmagupta também demonstrou regras para trabalhar com números negativos. Ele se referia a números positivos como fortunas e números negativos como dívidas. Ele escreveu regras como:"Uma fortuna subtraída de zero é uma dívida, "e" uma dívida subtraída de zero é uma fortuna ".
p Esta última afirmação é a mesma que a regra que aprendemos na escola, que se você subtrair um número negativo, é o mesmo que adicionar um número positivo. Brahmagupta também sabia que "O produto de uma dívida e uma fortuna é uma dívida" - um número positivo multiplicado por um negativo é um negativo.
p Em grande parte, Os matemáticos europeus relutavam em aceitar os números negativos como significativos. Muitos consideraram que os números negativos eram absurdos. Eles raciocinaram que os números foram desenvolvidos para contar e questionaram o que você poderia contar com números negativos. Os matemáticos indianos e chineses reconheceram desde o início que uma das respostas a essa pergunta eram as dívidas.
p Por exemplo, em um contexto de agricultura primitiva, se um fazendeiro deve a outro fazendeiro 7 vacas, então, efetivamente, o primeiro fazendeiro tem -7 vacas. Se o primeiro fazendeiro sai para comprar alguns animais para pagar sua dívida, ele tem que comprar 7 vacas e entregá-las ao segundo fazendeiro para que seu cálculo de vacas volte a 0. A partir de então, cada vaca que ele compra vai para seu total positivo.
p
Base para cálculo
p Essa relutância em adotar números negativos, e de fato zero, segurou a matemática européia por muitos anos. Gottfried Wilhelm Leibniz foi um dos primeiros europeus a usar o zero e os negativos de forma sistemática em seu desenvolvimento do cálculo no final do século XVII. O cálculo é usado para medir taxas de mudanças e é importante em quase todos os ramos da ciência, notavelmente sustentando muitas descobertas importantes na física moderna.
p Mas o matemático indiano Bhāskara já havia descoberto muitas das idéias de Leibniz mais de 500 anos antes. Bhāskara, também fez grandes contribuições para a álgebra, aritmética, geometria e trigonometria. Ele forneceu muitos resultados, por exemplo, nas soluções de certas equações "Doiphantine", que não seria redescoberto na Europa por séculos.
p A escola de astronomia e matemática de Kerala, fundada por Madhava de Sangamagrama em 1300, foi responsável por muitos primeiros na matemática, incluindo o uso de indução matemática e alguns resultados iniciais relacionados ao cálculo. Embora nenhuma regra sistemática para cálculo tenha sido desenvolvida pela escola de Kerala, seus proponentes primeiro conceberam muitos dos resultados que mais tarde seriam repetidos na Europa, incluindo as expansões da série de Taylor, infinitosimais e diferenciação.
p O salto, feito na Índia, que transformou o zero de um simples espaço reservado para um número por si só indica a cultura matematicamente iluminada que estava florescendo no subcontinente em uma época em que a Europa estava presa na idade das trevas. Embora sua reputação sofra com o viés eurocêntrico, o subcontinente tem uma forte herança matemática, que continua no século 21, fornecendo jogadores-chave na vanguarda de todos os ramos da matemática. p Este artigo foi publicado originalmente em The Conversation. Leia o artigo original.



