Este artigo mostrará como Esbocar os gráficos da Função Raiz Quadrada usando apenas três valores diferentes para 'x', depois encontrando os Pontos através dos quais o gráfico das Equações /Funções são desenhados, também mostrará como os Gráficos Traduz Verticalmente (move para cima ou para baixo), Horizontally Translates (move para a esquerda ou para a direita) e como o Graph faz simultaneamente Both Translations.
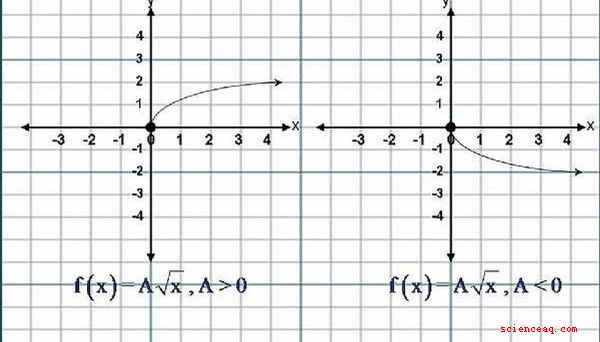
A Equação de uma Função de Raiz Quadrada possui o Form .. y = f (x) = A√x, onde (A) não deve ser igual a zero (0) .Se (A) for maior que Zero (0), ou seja, (A) é um Número Positivo, então, A forma do gráfico da função raiz quadrada é semelhante à metade superior da letra 'C'. Se (A) for menor que zero (0), ou seja, (A) é um número negativo, a forma do gráfico é semelhante à metade inferior da letra 'C'. Por favor, clique na imagem para uma melhor visualização.
Para esboçar o gráfico da equação, ... y = f (x) = A√x, escolhemos três valores para 'x', x = ( -1), x = (0) e x = (1). Nós substituímos cada valor de 'x' na Equação, ... y = f (x) = A√x e obtemos o respectivo valor correspondente para cada 'y'.
Dado y = f (x) = A√x, onde (A) é um Número Real e (A) diferente de Zero (0), e substituindo, x = (-1) na Equação, obtemos y = f (-1) = A√ ( -1) = i (que é um número imaginário). Portanto, o primeiro ponto não tem coordenadas reais, portanto, nenhum gráfico pode ser desenhado através desse ponto. Agora Substituindo, x = (0), obtemos y = f (0) = A√ (0) = A (0) = 0. Assim, o Segundo Ponto tem Coordenadas (0,0). E substituindo x = (1) obtemos y = f (1) = A√ (1) = A (1) = A. Portanto, o Terceiro Ponto tem Coordenadas (1, A). Como o primeiro ponto tinha coordenadas que não eram reais, agora procuramos um quarto ponto e escolhemos x = (2). Agora substitua x = (2) em y = f (2) = A√ (2) = A (1,41) = 1,41A. Então o quarto ponto tem coordenadas (2,1.41A). Agora esboçamos a curva através destes três pontos. Por favor, clique na imagem para uma melhor visão.
Dada a equação y = f (x) = A√x + B, onde B é qualquer número real, o gráfico desta equação seria traduzir verticalmente (B) unidades. Se (B) for um Número Positivo, o Gráfico moverá para cima (B) unidades, e se (B) for um Número Negativo, o Gráfico moverá para baixo (B) unidades. Para esboçar os gráficos desta equação, seguimos as instruções e usamos os mesmos valores de 'x' do passo # 3. Por favor, clique na imagem para ter uma visão melhor.
Dada a Equação y = f (x) = A√ (x - B) onde A e B são quaisquer Números Reais, e (A) não é igual a Zero (0), e x ≥ B. O gráfico desta equação iria traduzir horizontalmente (B) unidades. Se (B) for um Número Positivo, o Gráfico moverá para as unidades Direita (B) e se (B) for um Número Negativo, o Gráfico moverá para as unidades Esquerda (B). Para esboçar os gráficos desta equação, primeiro definimos a expressão, 'x - B', que está sob o sinal de radical Maior que ou Igual a zero, e resolvemos para 'x'. Isto é, ... x - B ≥ 0, depois x ≥ B.
Vamos agora usar os seguintes Três Valores para 'x', x = (B), x = (B + 1) e x = (B + 2). Nós substituímos cada valor de 'x' na Equação, ... y = f (x) = A√ (x - B) e obtemos o respectivo valor correspondente para cada 'y'.
Dado y = f (x) = A√ (x - B), onde A e B são números reais, e (A) não é igual a zero (o) onde x ≥ B. Substituindo, x = (B) na equação = f (B) = A√ (BB) = A√ (0) = A (0) = 0. Portanto, o primeiro ponto tem coordenadas (B, 0). Agora Substituindo, x = (B + 1), obtemos y = f (B + 1) = A√ (B + 1 - B) = A√1 = A (1) = A. Assim, o Segundo Ponto tem Coordenadas ( B + 1, A), e Substituindo x = (B + 2) obtemos y = f (B + 2) = A√ (B + 2-B) = A√ (2) = A (1,41) = 1,41A . Então o terceiro ponto tem coordenadas (B + 2,1.41A). Agora esboçamos a curva através destes três pontos. Por favor, clique na imagem para uma melhor visualização.
Dado y = f (x) = A√ (x - B) + C, onde A, B, C são números reais e (A) não é igual a Zero (0) e x ≥ B. Se C for um Número Positivo, o Gráfico no PASSO # 7 Traduzirá Verticalmente (C). Se (C) for um Número Positivo, o Gráfico moverá para cima (C), e se (C) for um Número Negativo, o Gráfico moverá para baixo (C) unidades. Para esboçar os gráficos desta equação, seguimos as instruções e usamos os mesmos valores de 'x' do passo # 7. Por favor, clique na imagem para ter uma visão melhor.