Autocorrelação é um método estatístico usado para análise de séries temporais. O objetivo é medir a correlação de dois valores no mesmo conjunto de dados em diferentes etapas de tempo. Embora os dados de tempo não sejam usados ​​para calcular a autocorrelação, seus incrementos de tempo devem ser iguais para obter resultados significativos. O coeficiente de autocorrelação serve a dois propósitos. Pode detectar não-aleatoriedade em um conjunto de dados. Se os valores no conjunto de dados não forem aleatórios, a autocorrelação pode ajudar o analista a escolher um modelo de série temporal apropriado.

Calcule a média, ou a média, dos dados que você está analisando. A média é a soma de todos os valores de dados divididos pelo número de valores de dados (n).

Decida um intervalo de tempo (k) para o seu cálculo. O valor de retardo é um inteiro denotando quantas etapas de tempo separam um valor do outro. Por exemplo, o atraso entre (y1, t1) e (y6, t6) é cinco, porque existem 6 - 1 = 5 intervalos de tempo entre os dois valores. Ao testar a aleatoriedade, você normalmente calculará apenas um coeficiente de autocorrelação usando defasagem k = 1, embora outros valores de defasagem também funcionem. Ao determinar um modelo de série temporal apropriado, você precisará calcular uma série de valores de autocorrelação, usando um valor de retardo diferente para cada um.

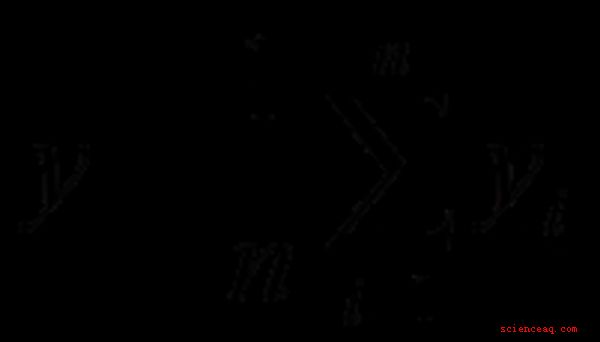
Calcule a função de autocovariância usando a fórmula fornecida. Por exemplo, se você estava calculando a terceira iteração (i = 3) usando um atraso k = 7, então o cálculo para essa iteração seria semelhante a: (y3 - y-bar) (y10 - y-bar) Iterar todos valores de "i" e, em seguida, pegue a soma e divida-o pelo número de valores no conjunto de dados.

Calcule a função de variância usando a fórmula fornecida. O cálculo é semelhante ao da função de autocovariância, mas o atraso não é usado.

Divida a função de autocovariação pela função de variância para obter o coeficiente de autocorrelação. Você pode ignorar esta etapa dividindo as fórmulas para as duas funções como mostrado, mas muitas vezes, você precisará da autocovariância e da variância para outros propósitos, portanto, é prático calculá-las individualmente também.