Cientistas investigam propagação de informações em sistemas bosônicos em interação
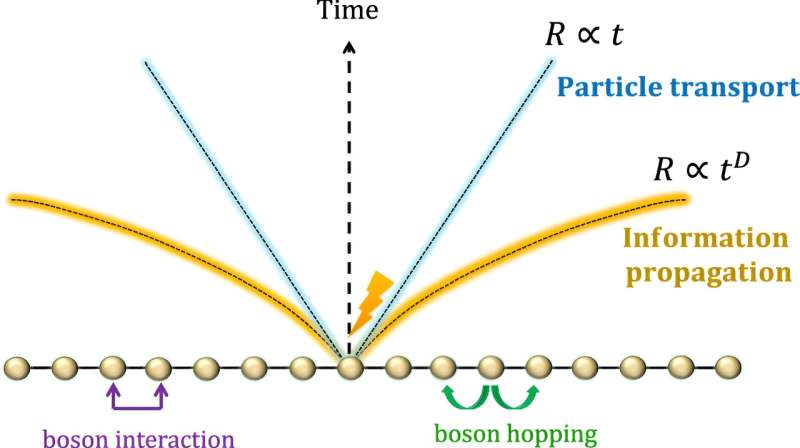Ilustração dos cones de luz efetivos. Aqui, descrevemos os bósons interagentes pelo Hamiltoniano do tipo Bose-Hubbard (1). Primeiro consideramos a rapidez com que as partículas de bóson se movem para regiões distantes, como mostrado na Fig. 2. O cone de luz para o transporte de partículas de bóson provou ser quase linear até correções logarítmicas (denotadas pela linha sombreada azul), como mostrado no Resultado 1. Por outro lado, se considerarmos a propagação da informação completa (ver também Fig. 3), a velocidade pode ser muito mais rápida que o transporte de partículas. O cone de luz efetivo é provado ser polinomial com o tempo, e o expoente é igual à dimensão espacial D (denotada pela linha sombreada laranja), onde a forma matemática do limite de Lieb-Robinson é dada no Resultado 2. Podemos explicitamente construir um protocolo para obter o cone de luz usando dinâmica com hamiltoniano do tipo Bose-Hubbard dependente do tempo. Crédito:Nature Communications (2024). DOI:10.1038/s41467-024-46501-7 Um novo estudo realizado por cientistas do Japão explora a propagação de informação quântica em sistemas de bósons em interação, como os condensados de Bose-Einstein (BECs), revelando o potencial de transmissão acelerada, ao contrário do que se pensava anteriormente.
Os sistemas quânticos de muitos corpos, como os sistemas de bósons em interação, são fundamentalmente importantes, pois encontram aplicações em vários ramos da física. A propagação da informação em sistemas quânticos de muitos corpos é governada pelo limite de Lieb-Robinson. Isso quantifica a rapidez com que as informações ou mudanças se propagam através de um sistema quântico.
Quando você faz uma alteração em uma parte do sistema, o limite de Lieb-Robinson descreve a velocidade com que essa alteração influencia outras partes do sistema. Em termos práticos, significa que o efeito da sua mudança inicial se espalhará para fora do seu ponto de origem, afectando regiões vizinhas do sistema.
No entanto, o caminho de Lieb-Robinson para sistemas de bósons em interação continua sendo um desafio há muito tempo.
Os pesquisadores, liderados pelo Dr. Tomotaka Kuwahara, líder da equipe RIKEN Hakubi no Centro RIKEN de Computação Quântica, abordam esse desafio em seu novo Nature Communications. estudar.
Kuwahara explicou a importância de seu trabalho ao Phys.org, destacando a importância de compreender os sistemas quânticos contendo partículas fundamentais como bósons e férmions.
“Os sistemas de bósons não têm, em princípio, nenhum limite de energia, o que tornou a ligação de Lieb-Robinson aos sistemas bosônicos significativamente desafiadora”, disse ele.
A ligação Lieb-Robinson
Conforme mencionado anteriormente, o limite de Lieb-Robinson fornece um limite quantitativo para a rapidez com que correlações ou influências podem se espalhar entre regiões espacialmente separadas de um sistema quântico.
O que isto significa é que a propagação não pode ocorrer instantaneamente em todos os lugares e, em vez disso, está limitada a um cone de luz efetivo. Inspirado na teoria da relatividade de Einstein, o cone de luz representa todos os pontos do espaço e do tempo que um sinal luminoso emitido por um evento pode atingir. Isto cria um cone duplo:um para o passado e outro para o futuro.
O mesmo se aplica à propagação de informação em sistemas quânticos de muitos corpos, ou seja, sistemas com mais de duas partículas quânticas.
“O limite Lieb-Robinson estabelece um limite de velocidade universal para a rapidez com que a informação pode viajar nestes sistemas”, explicou o Dr.
De acordo com o limite de Lieb-Robinson, a propagação da informação é limitada e decai exponencialmente com a distância ou o tempo. As especificidades do decaimento dependem do sistema individual e das interações que podem ocorrer dentro do sistema.
Formulado por Elliott Lieb e Derek Robinson em 1972, o limite de Lieb-Robinson só é aplicável a sistemas não relativísticos, o que significa que a informação viaja a velocidades muito inferiores à velocidade da luz.
O modelo Bose-Hubbard
Os sistemas de bósons em interação consistem em muitos bósons (como fótons). Esses sistemas, embora comuns, apresentam muitos desafios, como interações de longo alcance entre bósons e energia ilimitada, dificultando o desenvolvimento de simulações e modelos teóricos.
Mas, desde a descoberta do BEC, modelos como o modelo Bose-Hubbard foram desenvolvidos para estudar sistemas bosônicos. O modelo Bose-Hubbard é uma estrutura teórica usada para entender como os bósons se comportam quando confinados a uma estrutura de rede, como os átomos de um cristal.
Este modelo leva em consideração dois fatores principais. O primeiro é o salto de bósons de um local da rede para outro, representado pelo parâmetro de salto. O segundo é o parâmetro de interação no local, que representa as forças repulsivas entre os bósons quando ocupam o mesmo local. Esta energia de interação aumenta à medida que mais bósons ocupam o mesmo local.
Esses fatores incorporam a interação entre os bósons, razão pela qual os pesquisadores escolheram o modelo de Bose-Hubbard para investigar os limites de Lieb-Robinson em sistemas de bósons em interação.
Os limites superiores
Os pesquisadores optaram por estudar o limite de Lieb-Robinson para uma rede D-dimensional (sistema de bósons interativos) governado pelo modelo de Bose-Hubbard. Eles encontraram três resultados para este sistema.
Resultado 1
Este resultado aborda a interação dos bósons dentro da rede. Os investigadores descobriram que a velocidade do transporte de bósons é limitada, mesmo em sistemas com interações de longo alcance. Esta velocidade, embora limitada, cresce no máximo logaritmicamente com o tempo, o que é relativamente lento.
Esta descoberta fornece informações cruciais sobre a dinâmica dos sistemas de bósons, colocando um limite superior na sua velocidade.
Resultado 2
Este resultado foca na propagação dos operadores do sistema ao longo do tempo. Os operadores são basicamente variáveis do sistema, como o momento. À medida que estes operadores se propagam, eles se desviam da evolução ideal, levando ao acúmulo de erros.
Essa propagação de erro determina a rapidez com que as informações podem se propagar no sistema. Por exemplo, se o erro for grande, indica que a propagação da informação é mais lenta ou mais restrita, pois a aproximação se desvia significativamente da evolução ideal do sistema.
Da mesma forma, se o erro for pequeno, a propagação da informação será rápida. Isto se alinha com o limite de Lieb-Robinson, indicando a presença de um limite superior na propagação do erro.
Apesar da presença de um limite superior na propagação do erro, as interações entre os bósons induzem o agrupamento em regiões específicas. Estas regiões, caracterizadas por concentrações mais elevadas de bósons, facilitam a propagação acelerada de informações ao longo de certos caminhos ou direções da rede.
Este fenômeno está alinhado com o limite de Lieb-Robinson. Porém, esta aceleração é limitada e tem um crescimento polinomial dependendo da dimensionalidade do sistema.
Resultado 3
Este resultado apresenta uma forma de simular esses sistemas utilizando portas quânticas elementares (como CNOT). Os pesquisadores fornecem um limite superior para o número de portas quânticas elementares necessárias para simular com eficiência a evolução temporal de sistemas de bósons em interação.
Comparação com sistemas fermiônicos
Os sistemas fermiônicos mostram um limite de velocidade finito para a rapidez com que a informação pode se propagar. Antes deste trabalho, os cientistas presumiam o mesmo para os sistemas bosônicos, o que não é verdade.
"O cone de luz se espalha muito mais rápido e não é linear, ou seja, acelera com o tempo. Especificamente, se você estiver olhando para um espaço tridimensional, a distância que a 'informação' pode viajar aumenta com o quadrado do tempo. Portanto, neste sentido, os bósons podem enviar informações muito mais rapidamente do que os férmions, especialmente com o passar do tempo", explicou o Dr. Kuwahara.
Isto depende do número de bósons que podem ocupar o mesmo estado ao mesmo tempo. Essencialmente, quanto mais bósons se juntarem, mais rápida a informação poderá se propagar.
"Mas, como os bósons só podem se mover a uma velocidade finita, leva um pouco de tempo para que muitos deles se juntem, levando a uma velocidade limitada de propagação da informação. Com o tempo, à medida que mais bósons cooperam, a velocidade com que eles pode enviar informações aumenta", disse o Dr. Kuwahara.
Este trabalho abre uma nova janela para a exploração de sistemas de bósons interativos para propagação de informação.
"Prevejo que o algoritmo será usado para simular a física da matéria condensada, o que poderia levar à descoberta de novas fases quânticas. Também deverá ser útil na simulação da termalização quântica, ajudando a resolver a questão básica de como os sistemas quânticos fechados se estabelecem em um estado estacionário ao longo do tempo", concluiu o Dr. Kuwahara.
