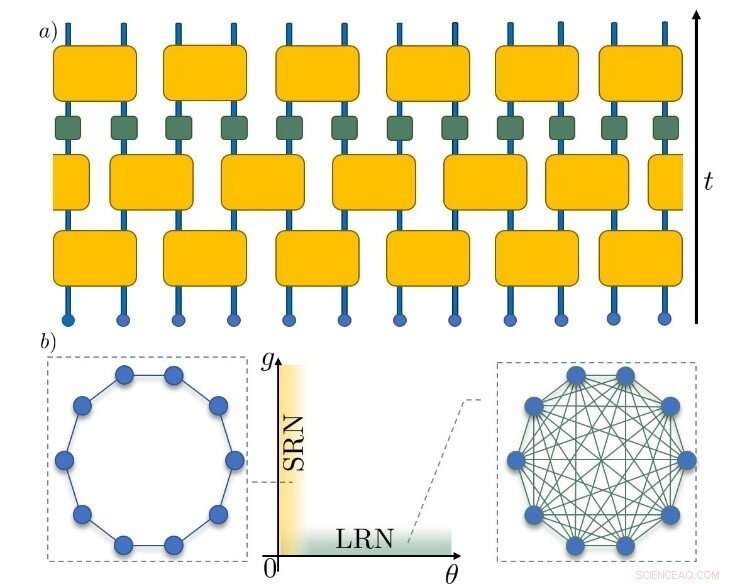
Figura 1. Representação esquemática do modelo de Mapa de Circuito Unitário. (a) A seta preta à direita mostra a direção do tempo à medida que as partículas, representadas por pequenos círculos azuis, evoluem. Os quadrados amarelos representam as transformações que acoplam as partículas. Os quadrados verdes indicam as transformações não lineares indutoras do caos. (b) Dependendo dos parâmetros selecionados, o acoplamento entre partículas pode ser de curto alcance (esquerda) ou de longo alcance (direita). Isso acaba afetando as escalas de tempo emergentes da dinâmica caótica. Crédito:Instituto de Ciências Básicas
Um exemplo popular de comportamento caótico é o efeito borboleta – uma borboleta pode bater as asas em algum lugar do Oceano Atlântico e causar um tornado no Colorado. Esta fábula notável ilustra como a extrema sensibilidade da dinâmica de sistemas caóticos pode produzir resultados dramaticamente diferentes, apesar de pequenas diferenças nas condições iniciais. As leis fundamentais da natureza que governam a dinâmica dos sistemas físicos são inerentemente não lineares, muitas vezes levando ao caos e à termalização subsequente.
No entanto, pode-se perguntar por que não há aumento desenfreado de tornados no Colorado causados por uma enorme decepção de borboletas em assuntos globais, como o aquecimento global? Isso porque a dinâmica física, embora caótica, é capaz de demonstrar estados notavelmente estáveis. Um exemplo é a estabilidade do nosso sistema solar – ele obedece às leis não lineares da física, que aparentemente podem induzir o caos no sistema.
A razão para esta estabilidade reside no fato de que sistemas fracamente caóticos podem apresentar dinâmicas periódicas muito ordenadas que podem durar milhões de anos. Essa descoberta foi feita na década de 1950 pelos grandes matemáticos Kolmogorov, Arnold e Moser. Sua descoberta, no entanto, funciona apenas no caso de sistemas com um pequeno número de elementos em interação. Se o sistema inclui muitas partes constituintes, então seu destino não é tão bem compreendido.
Pesquisadores do Centro de Física Teórica de Sistemas Complexos (PCS) do Instituto de Ciências Básicas (IBS), Coréia do Sul, introduziram recentemente uma nova estrutura para caracterizar dinâmicas fracamente caóticas em sistemas complexos contendo um grande número de partículas constituintes. Para conseguir isso, eles usaram um modelo baseado em computação quântica – Mapa de Circuitos Unitários – para simular o caos.
Investigar escalas de tempo de caoticidade é uma tarefa desafiadora, exigindo métodos computacionais eficientes. O modelo de Mapa de Circuito Unitário implementado neste estudo atende a esse requisito. "O modelo permite a propagação eficiente e sem erros de estados no tempo", explica Merab Malishava, "o que é essencial para modelar uma caoticidade extremamente fraca em grandes sistemas. Esses modelos foram usados para atingir tempos recordes de evolução não linear antes, o que era também feito em nosso grupo."
Como resultado, eles foram capazes de classificar a dinâmica dentro do sistema, identificando as escalas de tempo e comprimento que surgem à medida que a termalização diminui drasticamente. Os pesquisadores descobriram que, se as partes constituintes estiverem conectadas em uma rede de longo alcance (LRN) (por exemplo, de maneira geral), a dinâmica da termalização será caracterizada por uma escala de tempo única, chamada de tempo Lyapunov. No entanto, se o acoplamento for de natureza de rede de curto alcance (SRN) (por exemplo, vizinho mais próximo), surge uma escala de comprimento adicional relacionada ao congelamento de partes maiores do sistema por longos períodos com raros respingos caóticos.
Normalmente os estudos sobre essa dinâmica sensível são feitos usando as técnicas de análise do comportamento de observáveis. Essas técnicas datam da década de 1950, quando foram realizados os primeiros experimentos sobre caoticidade e termalização. Os autores identificaram um novo método de análise – investigando a escala do espectro de Lyapunov.
Merab Malishava diz:"Métodos anteriores podem resultar em resultados ambíguos. Você escolhe uma termalização observável e aparentemente percebe e pensa que a dinâmica é caótica. No entanto, se outro observável for estudado, de outra perspectiva, você conclui que o sistema está congelado e nada O espectro de Lyapunov é um conjunto de escalas de tempo que caracterizam a dinâmica total e completamente. Além disso, é o mesmo de todos os pontos de vista!
Os resultados não são apenas interessantes do ponto de vista fundamental. Eles também têm o potencial de lançar luz sobre as realizações dos computadores quânticos. A computação quântica requer uma dinâmica coerente, o que significa que não há termalização. No trabalho atual, uma desaceleração dramática da dinâmica térmica foi estudada com quantidades emergentes quase conservadas. A quantificação deste caso poderia explicar fenômenos como a localização de muitos corpos, que é uma das ideias básicas para evitar a termalização em computadores quânticos.
Outra grande conquista do estudo diz respeito à aplicabilidade dos resultados a uma grande maioria de modelos físicos que vão desde redes de osciladores simples até dinâmicas de redes de spin complexas. Dr. Sergej Flach, líder do grupo de pesquisa e diretor do PCS explica:"Estamos trabalhando há cinco anos no desenvolvimento de uma estrutura para classificar dinâmicas fracamente caóticas em sistemas macroscópicos, o que resultou em uma série de trabalhos avançando significativamente na área . Deixamos de lado estudos caso a caso com foco restrito em favor da promoção de uma abordagem conceitual confiável e relacionável em um grande número de realizações físicas. Este trabalho específico é um bloco de construção muito importante na estrutura mencionada. Descobrimos que um A maneira tradicional de ver as coisas às vezes não é a mais informativa e oferece uma nova abordagem alternativa. Nosso trabalho não pára aqui, pois esperamos avançar na ciência com mais ideias inovadoras."
Esta pesquisa foi publicada recentemente em
Physical Review Letters. + Explorar mais Congelamento por aquecimento:Formação de vidro dinâmico
