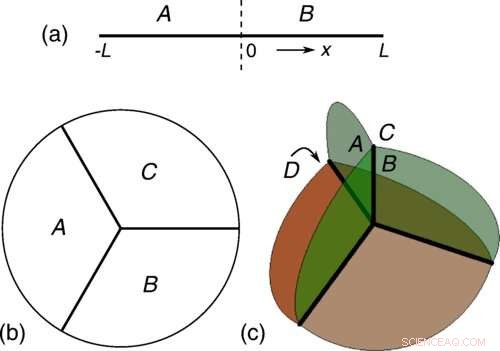
O gás de Fermi D-dimensional para (a) D=1, (b) D=2 e (c) D=3 é particionado em regiões D+1 que se encontram em um único ponto, com quaisquer k regiões compartilhando um limite plano de dimensão D + 1 - k. Aqui estudamos uma medida de emaranhamento, conhecida como informação mútua, que captura as correlações intrínsecas entre todas as regiões D + 1. A informação mútua é topológica na medida em que exibe uma divergência logarítmica principal proporcional à característica de Euler χF do mar de Fermi. Crédito:Pok Man Tam et al, Revisão Física X (2022). DOI:10.1103/PhysRevX.12.031022
Topologia e emaranhamento são dois princípios poderosos para caracterizar a estrutura de estados quânticos complexos. Em um novo artigo na revista
Physical Review X , pesquisadores da Universidade da Pensilvânia estabelecem uma relação entre os dois.
"Nosso trabalho une duas grandes idéias", diz Charles Kane, Christopher H. Browne Distinguished Professor of Physics na Penn's School of Arts &Sciences. "É uma ligação conceitual entre topologia, que é uma forma de caracterizar as características universais que os estados quânticos têm, e o emaranhamento, que é uma maneira pela qual os estados quânticos podem exibir correlações não locais, onde algo que acontece em um ponto no espaço é correlacionado com algo que acontece em outra parte do espaço. O que encontramos é uma situação em que esses conceitos estão intimamente interligados."
A semente para explorar essa conexão veio durante as longas horas que Kane passou em seu escritório em casa durante a pandemia, ponderando novas ideias. Uma linha de pensamento o fez imaginar a imagem clássica de livro didático da superfície de Fermi do cobre, que representa as energias potenciais dos elétrons do metal. É uma imagem que todo estudante de física vê e com a qual Kane estava muito familiarizado.
"Claro, eu aprendi sobre essa imagem na década de 1980, mas nunca pensei nela como uma descrição de uma superfície topológica", diz Kane.
Uma maneira clássica de pensar sobre superfícies topológicas, diz Kane, é considerar a diferença entre um donut e uma esfera. Qual é a diferença? Um único buraco. A topologia considera essas propriedades generalizáveis de uma superfície, que não são alteradas pela deformação. Sob este princípio, uma xícara de café e um donut teriam a mesma propriedade topológica.
Considerando a superfície de Fermi do cobre como um objeto topológico, então, o número associado de buracos que ela possui é quatro, figura também conhecida como gênero. Uma vez que Kane começou a pensar na superfície de Fermi dessa maneira, ele se perguntou se poderia existir uma relação entre o gênero e o emaranhamento quântico.
Para investigar ainda mais essa possível conexão, Kane envolveu seu aluno de pós-graduação Pok Man Tam e Martin Claassen, professor assistente de física da Penn, que se concentrou no emaranhamento quântico em seu trabalho. Juntos, eles derivaram uma relação matemática entre o gênero da superfície de Fermi e uma medida de emaranhamento quântico chamada de informação mútua. A informação mútua caracteriza as correlações que podem ocorrer em regiões díspares do espaço que se encontram em um único ponto. Um número conhecido como característica de Euler, que está intimamente relacionado ao gênero, forneceu a conexão precisa entre os dois.
Os pesquisadores estabeleceram que a relação entre topologia e emaranhamento realizada em um sistema metálico simples, com elétrons se movendo independentemente um do outro, estendeu sua análise para mostrar que a conexão também estava presente mesmo quando os elétrons interagiam com maior complexidade.
E embora o trabalho teórico tenha sido feito em metais, Kane acredita que se estenderá a outros materiais também, como aqueles que envolvem interações muito fortes entre elétrons.
“O que isso pode nos permitir é criar novas maneiras de pensar sobre as fases da matéria que não entendemos muito bem e não temos tantas ferramentas para explorar”, diz Kane. "As pessoas estão tentando descobrir como alavancar a mecânica quântica para tirar proveito da informação quântica. Para fazer isso, você precisa entender como a mecânica quântica se manifesta quando você tem muitos graus de liberdade. Esse é um problema muito difícil, e isso trabalho está nos empurrando nessa direção."
No trabalho de acompanhamento, Kane e seus colegas esperam projetar experimentos que continuem a explorar o link recém-descoberto, talvez desenvolvendo uma nova técnica para medir o gênero topológico e uma maneira de investigar a estrutura do emaranhamento quântico.
+ Explorar mais Physicists find signatures of highly entangled quantum matter
