
Crédito CC0:domínio público
Supercondutores topológicos (TSCs) são novos tipos de estados quânticos topológicos com estrutura de banda gapped totalmente supercondutora na massa, mas eles suportam excitações sem intervalos chamados modos zero Majorana (MZMs) nos limites. Por causa de sua correlação não local e natureza estatística não Abeliana, Os MZMs são propostos como os qubits da computação quântica topológica. Portanto, pesquisar e operar os MZMs em materiais TSC é agora um tópico importante na física da matéria condensada.
Para identificar um TSC, deve-se primeiro verificar sua classificação topológica. A classificação topológica depende altamente das simetrias, incluindo simetria de reversão do tempo, simetria partícula-buraco, e especialmente as simetrias cristalinas. Sem a consideração de simetrias cristalinas, os Hamiltonianos de Bogoliubov-deGennes (BdG) dos supercondutores 1-D têm apenas a classificação Z2. A simetria de reflexão de espelho e simetrias rotacionais podem melhorar a classificação para a classe Z. No entanto, a classificação topológica de supercondutores com simetrias magnéticas gerais ainda é uma questão em aberto.
Em um novo artigo de pesquisa publicado no National Science Review , cientistas da Universidade Huazhong de Ciência e Tecnologia em Wuhan, China, e a Princeton University em New Jersey, Os EUA propuseram o método para classificar a fase supercondutora topológica examinando a compatibilidade entre diferentes MZMs. Co-autores Jinyu Zou, Qing Xie, Zhida Song e Gang Xu analisaram a classificação topológica de fios supercondutores gapped com simetrias magnéticas locais (LMSs). Eles descobriram que um TSC de classe BDI eficaz pode ser realizado em M x T ou C 2z Fio T invariante. Notavelmente, as novas fases do TSC caracterizadas por Zh invariante em C 4z O caso T e o invariante Zhoplus Zc no caso C6zT são descobertos.
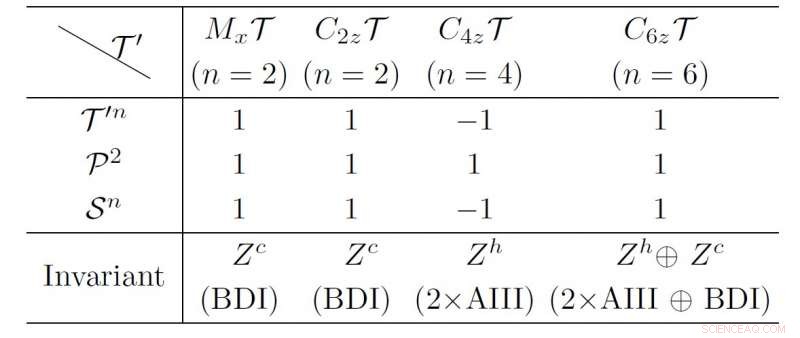
A classificação topológica dos sistemas supercondutores gapped 1D com os LMSs. Crédito:© Science China Press
No artigo intitulado "Novos tipos de supercondutores topológicos sob simetrias magnéticas locais". Os autores se concentram nos fios supercondutores 1D com LMSs T '=M x T, C 2z T, C 4z T e C 6z T. "A operação de T 'não muda a posição dos elétrons. Portanto, ela atua no hamiltoniano BdG como um operador de reversão no tempo". Combinar T 'e a simetria do buraco da partícula P leva a uma simetria quiral S =T'P. O hamiltoniano BdG pode adotar a forma diagonalizada de acordo com a simetria quiral. E os MZMs são os próprios estados da simetria quiral S. Os autores descobriram que "MZMs com autovalores quirais s e -s podem se acoplar e ser eliminados." Seguindo a diretriz, eles analisam a compatibilidade dos MZMs no final dos fios supercondutores 1D com LMSs, e resumir sua classificação topológica conforme listado na Tabela I.
Eles x T e C 2z Casos T são equivalentes à classe BDI com invariante topológico quiral Zc. Enquanto o caso C4zT é caracterizado por Z helicoidal h invariante, que indicam vários pares de Majorana Kramer na extremidade do fio supercondutor. No C 6z Caso T, "a topologia de todo o hamiltoniano BdG é classificada por Z h oplus Z c , ". Em uma nova fase topológica, "os MZMs helicoidais e quirais podem coexistir."
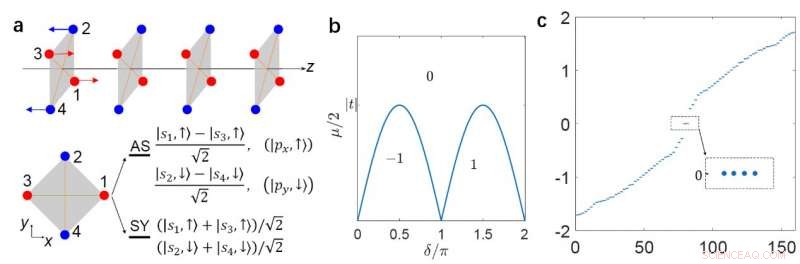
(a) Um fio supercondutor com preservação de C4zT alinhado ao longo da direção z. (b) O diagrama de fase topológico. (c) o espectro de fase não trivial com um limite aberto em ambos os lados, em que quatro MZMs aparecem com energia zero. Crédito:© Science China Press
"Para ilustrar a fase de TSC com o LMS C 4z T, construímos uma cadeia anti-ferromagnética 1D ao longo da direção z, "acrescentam os cientistas. Eles fornecem o diagrama de fase topológica do modelo." Na fase não trivial do TSC, o fio quântico aberto captura pares inteiros de MZMs em suas extremidades. "Eles também mostram os MZMs por meio de cálculos numéricos e analíticos.
"Esses resultados não apenas enriquecem a variedade do TSC 1-D, mas também fornecem blocos de construção luxuriantes para a construção de novos TSCs tipo 2-D e 3-D ", eles prevêem no final do artigo, "Por exemplo, pode-se acoplar os TSCs 1D na direção y para construir um TSC 2-D. As linhas de alta simetria ky =0 e ky =pi no espaço de momento preservam o 1D LMS. Com parâmetros adequados, as linhas ky =0 e ky =pi podem pertencer a fases topológicas distintas, e resultam na propagação contínua de estados de borda de Majorana conectando as bandas condutoras e as bandas de valência. "