Se você acompanha a cobertura da March Madness da Sciencing, sabe que estatísticas e números desempenham um papel enorme no torneio da NCAA.

A melhor parte? Você não precisa ser um fanático por esportes para trabalhar em alguns problemas matemáticos centrados nos esportes.

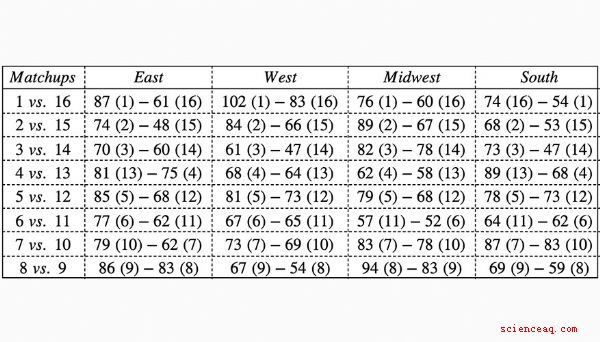
Criamos uma série de perguntas matemáticas que incorporam dados dos resultados do Madness de março do ano passado. A tabela abaixo mostra os resultados de cada partida das semifinais da Rodada de 64. Use-o para responder às perguntas de 1 a 5.

Se você não quiser ver as respostas, volte para a página original.

Boa sorte!
Perguntas sobre estatísticas:

Confira nossos artigos sobre média, mediana, modo e intervalo interquartil se precisar atualizar antes de começar.

Pergunta 1: Qual é a diferença média das pontuações em Região leste, oeste, centro-oeste e sul para a rodada loucura de 64 de março de 2018?

Pergunta 2: Qual é a diferença mediana das pontuações nas regiões leste, oeste, centro-oeste e sul da rodada loucura de 64 de março de 2018?

Pergunta 3: Qual é o IQR (Intervalo Interquartil) da diferença de pontuações nas regiões Leste, Oeste, Centro-Oeste e Sul para a Madness Round de 64 de março de 2018?

Pergunta 4: Quais matchups foram discrepantes em termos da diferença de pontuação?

Pergunta 5: Qual região foi mais "competitiva" na Rodada Madness de 64 de março de 2018? Qual métrica você usaria para responder a essa pergunta: média ou mediana? Por quê?

Competitividade:
Quanto menor a diferença entre ganhar e perder pontos, mais "competitivo" o jogo é. Por exemplo: se as pontuações finais de dois jogos foram 80-70 e 65-60, de acordo com nossa definição, o último jogo foi mais "competitivo".
Respostas de Estatísticas:

Pergunta 1 ( diferença de pontuação):

Leste: 26, 26, 10, 6, 17, 15, 17, 3
Oeste: 19, 18, 14, 4, 8, 2, 4, 13
Centro-Oeste: 16, 22, 4, 4, 11, 5, 5, 11
Sul: 20, 15, 26, 21, 5, 2, 4, 10

Questão 2 (média da diferença de pontuação):

Média \u003d Soma de todas as observações /Número de observações
Leste: (26 + 26 + 10 + 6 + 17 + 15 + 17 + 3 ) /8 \u003d 15
Oeste: (19 + 18 + 14 + 4 + 8 + 2 + 4 + 13) /8 \u003d 10,25
Centro-Oeste: (16 + 22 + 4 + 4 + 11 + 5 + 5 +11) /8 \u003d 9,75
Sul: (20 + 15 + 26 + 21 + 5 + 2 + 4 + 10) /8 \u003d 12,875

Pergunta 2 (mediana da diferença de pontuação ):

Mediana é o valor do percentil 50.

A mediana de uma lista pode ser encontrada organizando os números em ordem crescente e escolhendo o valor do meio. Aqui, como o número de valores é um número par (8), a mediana será a média dos dois valores médios, neste caso, a média do 4º e 5º valor.

Leste: Média de 15 e 17 \u003d 16
Oeste: Média de 8 e 13 \u003d 10,5 - Centro-Oeste: Média de 5 e 11 \u003d 8
Sul: Média de 10 e 15 \u003d 12,5

Pergunta 3 (IQR da diferença de pontuações):

O IQR é definido como a diferença entre o percentil 75 (Q3) e o valor percentual 25 (Q1).
\\ def \\ arraystretch {1.3} \\ begin {array} {|

c: c: c: c |

} \\ hline Region &Q1 &Q3 &IQR \\; (Q3-Q1) \\\\ \\ hline East &9 &19.25 &10.12 \\\\ \\ hdashline West &4 &15 &11 \\\\ \\ hdashline Midwest &4.75 &12.25 &7.5 \\\\ \\ hdashline Sul &4,75 &20,25 &15,5 \\\\ \\ hdashline \\ end {array}

Pergunta 4 (combinações outlier):

Outliers: qualquer valor que seja menor que Q1 - 1,5 x IQR ou superior a Q3 + 1,5 x IQR
\\ def \\ arraystretch {1.3} \\ begin {array} {|

c: c: c |

} \\ hline Region &Q1-1.5 \\ times IQR &Q3 + 1.5 \\ times IQR \\\\ \\ hline East &-6.375 &34.625 \\\\ \\ hdashline West &-12.5 &31.5 \\\\ \\ hdashline Midwest &-6.5 &23. 5 \\\\ \\ hdashline South &-18,5 &43,5 \\\\ \\ hline \\ end {array}

Não, outliers nos dados.

Pergunta 5 (região mais competitiva)
:

Ordem de competitividade usando a média: Centro-Oeste> Oeste> Sul> Leste
Ordem de competitividade usando a mediana: Centro-Oeste> Oeste> Sul> Leste

Como neste caso em particular não há Mas os alunos devem falar sobre o efeito dos valores discrepantes na média das observações.
Perguntas sobre Probabilidade

Confira nosso artigo sobre probabilidade binomial se precisar de uma atualização.

Lançamento livre: No basquete, lances livres ou chutes sujos são tentativas sem oposição de marcar pontos, arremessando por trás da linha de lance livre.

Assumindo que cada lance livre é um evento independente, o cálculo do sucesso no lance livre pode ser modelado pela Distribuição de Probabilidade Binomial. Aqui estão os dados dos lances livres feitos pelos jogadores no jogo do Campeonato Nacional de 2018 e sua probabilidade de acertar o lance livre para a temporada 2017-18 (observe que os números foram arredondados para o número decimal de um lugar mais próximo).
•• • Sciencing

Pergunta 1: Calcule a probabilidade de cada jogador receber o número determinado de lances livres bem-sucedidos no número de tentativas realizadas.

Resposta:

Distribuição de probabilidade binomial:
{{N} \\ escolha {k}} \\ cdot p ^ k (1-p) ^ {Nk}

Veja a resposta em uma tabela:
\\ def \\ arraystretch {1.3} \\ begin {array} {|

c: c |

} \\ hline \\ bold {Jogadores} &\\ bold {Probability} \\\\ \\ hline Moritz \\ Wagner &0,41 \\\\ \\ hdashline Charles \\; Matthews &0,0256 \\\\ \\ hdashline Zavier \\; Simpson &0,375 \\\\ \\ hdashline Muhammad- Ali \\; Abdur-Rahkman &0.393 \\\\ \\ hdashline Jordan \\; Poole \\ 0.8 \\ hdashline Eric \\; Paschall &0.32 \\\\ \\ hdashline Omari \\; Spellman &0.49 \\\\ \\ hdashline Mikal \\; Bridgers &0.64 \\\\ \\ hdashline Collin \\; Gillespie &0,41 \\\\ \\ hdashline Donte \\; DiVincenzo &0,2 \\ end {array}

Pergunta 2: Aqui estão os dados da sequência do tiro livre dos jogadores no mesmo jogo. 1 significa que o lance livre foi bem-sucedido e 0 significa que não obteve êxito.
••• Sciencing

Calcule a probabilidade de cada jogador acertar a seqüência exata acima. A probabilidade é diferente da calculada antes? Por que?

Resposta:
\\ def \\ arraystretch {1.3} \\ begin {array} {|

c: c |

} \\ hline \\ bold {Jogadores} &\\ bold {Probabilidade} \\\\ \\ hline Moritz \\; Wagner &0,64 \\\\ \\ hdashline Charles \\; Matthews &0,0256 \\\\ \\ hdashline Zavier \\; Simpson &0,125 \\\\ \\ hdashline Muhammad- Ali \\; Abdur-Rahkman &0,066 \\\\ \\ hdashline Jordan \\; Poole \\ 0,8 \\\\ \\ hdashline Eric \\; Paschall &0,16 \\ \\ \\ hdashline Omari \\; Spellman &0,49 \\\\ \\ hdashline Mikal \\; Bridgers &0,64 \\\\ \\ hdashline Collin \\; Gillespie &0,41 \\\\ \\ hdashline Donte \\; DiVincenzo &0,001 \\\\ \\ hline \\ end {array}

As probabilidades podem ser diferentes, pois na pergunta anterior não nos preocupamos com a ordem em que os lances livres foram feitos. Mas a probabilidade será a mesma nos casos em que houver apenas um pedido possível. Por exemplo:

Charles Matthews não conseguiu marcar um lance livre nas 4 tentativas e Collin Gillespie obteve sucesso nas 4 tentativas.
Pergunta sobre o bônus

Usando os números de probabilidade acima, responda estas perguntas:

1. Quais jogadores tiveram um dia ruim /ruim com seu arremesso de lance livre?
   
2. Quais jogadores tiveram um dia bom /ruim com seu arremesso de lance livre?
   < Resposta: Charles Matthews teve um dia de azar na linha de lance livre, já que a probabilidade dele perder todos os lances livres era de 0,0256 (havia apenas 2,5% de chance desse evento ocorrer).
   

   Sentindo o espírito da loucura de março? Confira nossas dicas e truques para preencher um suporte e leia por que é tão difícil prever problemas e escolher um suporte perfeito.