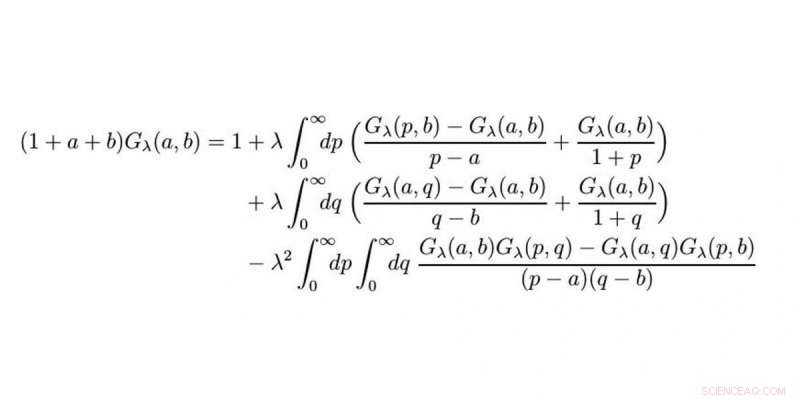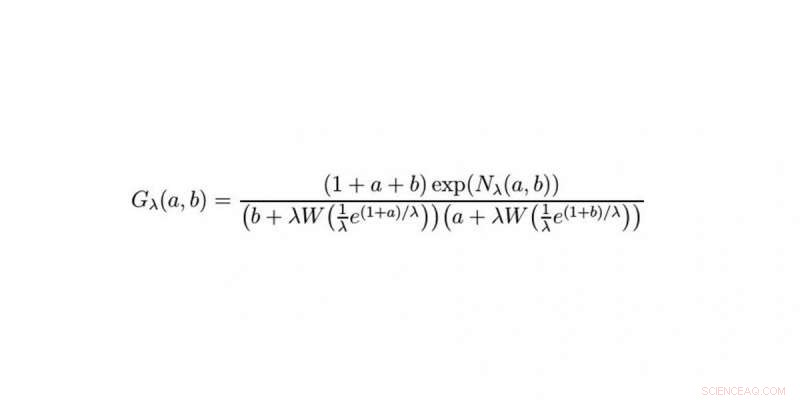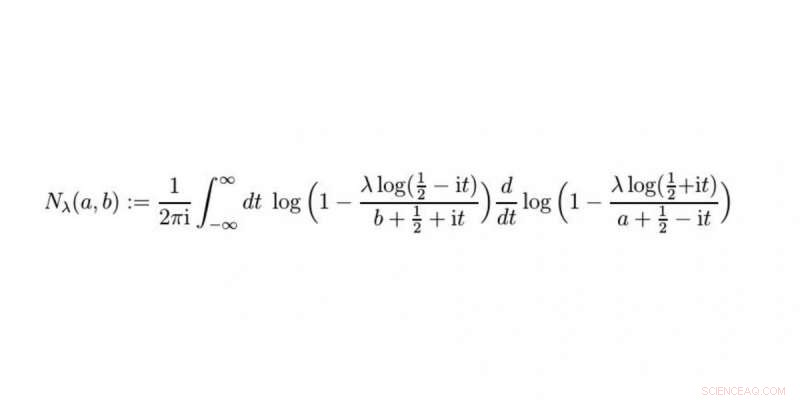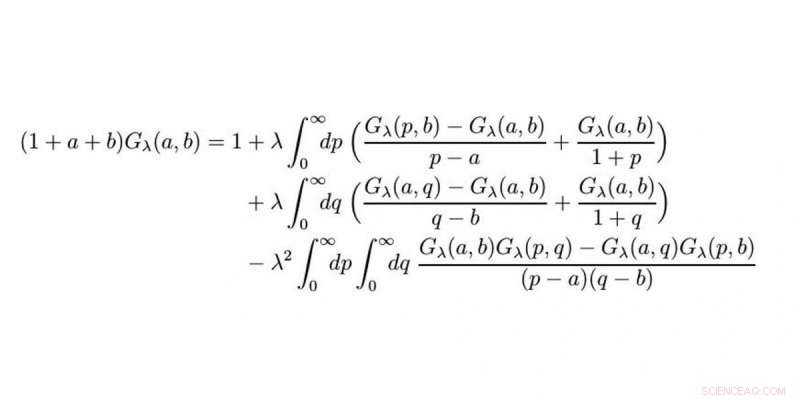 p A equação matemática. Crédito:WWU / Raimar Wulkenhaar
p A equação matemática. Crédito:WWU / Raimar Wulkenhaar
p Depois de 10 anos, O Prof. Raimar Wulkenhaar do Instituto de Matemática da Universidade de Münster e seu colega Dr. Erik Panzer da Universidade de Oxford resolveram uma equação matemática considerada insolúvel. A equação deve ser usada para encontrar respostas a perguntas feitas pela física de partículas elementares. Nesta entrevista com Christina Heimken, Wulkenhaar analisa os desafios encontrados ao buscar a fórmula para uma solução e explica por que o trabalho ainda não foi concluído. p
Você trabalhou na solução da equação por 10 anos. O que tornou essa equação tão difícil de resolver?
p É uma equação integral não linear com duas variáveis. Essa equação é tão complexa que você realmente pensa que não pode haver nenhuma fórmula para uma solução. Duas variáveis por si só são um desafio, e não há abordagens estabelecidas para encontrar uma solução para equações integrais não lineares. No entanto, repetidas vezes durante esses 10 anos, houve lampejos de esperança e, como resultado, e apesar de todas as dificuldades, Achei que encontrar uma fórmula explícita para uma solução - expressa por meio de funções conhecidas - era realmente possível.
p
Para que pode ser usada a equação?
p É sobre uma compreensão matemática das teorias quânticas de campo. Pertencem ao campo da física e participam de experimentos de grande escala, como os realizados no CERN. O objetivo é descrever matematicamente as partículas elementares, isto é, os menores componentes conhecidos da matéria. Mas isso é tão complicado que, em vez de, partículas imaginárias são descritas matematicamente, as quais têm certas propriedades das partículas reais. A esperança é que um dia as partículas reais possam ser descritas usando os métodos assim estabelecidos.
p
Depois de trabalhar no problema por 10 anos, você experimentou um avanço este ano. Como isso aconteceu?
p No final de maio, Tentei uma ideia para a qual meu Ph.D. aluna, Alexander Hock, forneceu o impulso decisivo. Elaborei uma nova equação - mais simples que a anterior - e comecei a resolvê-la em loops. Isso significa que você aborda a solução passo a passo, ou seja, loop por loop, calculando o lado esquerdo da equação em cada etapa anterior e usando-o para o lado direito da equação na próxima etapa.
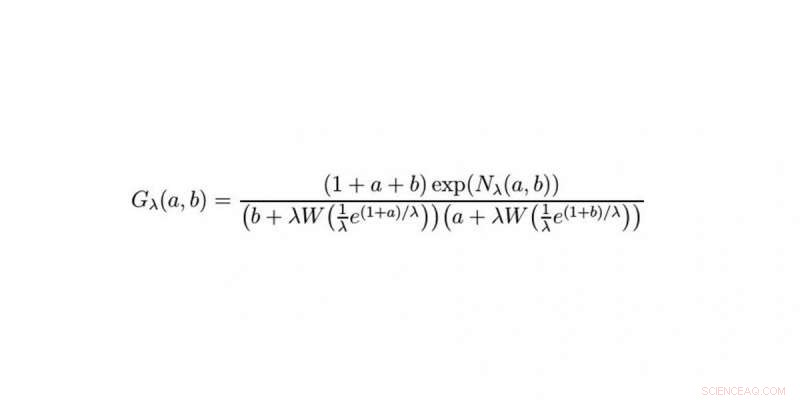 p A solução. Crédito:WWU / Raimar Wulkenhaar
p A solução. Crédito:WWU / Raimar Wulkenhaar
p No quarto loop, tive que calcular a soma de 46 integrais que continham, entre outras coisas, polilogaritmos. Esses polilogaritmos, que são algumas das funções mais exigentes, tornou-se mais complicado em cada loop. Eu tive sorte nisso, em suma, quase tudo foi cancelado, e o que restou foi apenas uma pequena soma de potências de logaritmos normais. Eu imediatamente percebi que havia um tesouro a ser encontrado aqui.
p O quinto loop não foi tão fácil de resolver - mas novamente tive sorte. Durante uma escola de verão nos Alpes franceses, tive a oportunidade de conversar com especialistas nessas funções. Um desses especialistas foi o Dr. Erik Panzer, da Universidade de Oxford. Ele havia escrito um programa de computador sobre a matemática simbólica dos hiperlogaritmos e forneceu suporte. Da noite para o dia, esse programa calculou minha equação até o sétimo loop. Ele confirmou meus resultados até o quarto ciclo, e após o quarto loop, o milagre continuou - tudo poderia ser dividido em logaritmos normais. Um padrão começou a surgir!
p
O que isso significa?
p Talvez você se lembre do Triângulo de Pascal de seus tempos de escola, com os coeficientes binominais? No triângulo, cada número inserido em uma linha do triângulo é a soma dos dois números inseridos acima dele. E é exatamente essa estrutura triangular que encontramos em nossos loops - embora mais complicada do que no triângulo de Pascal.
p Em 9 de junho, os loops oito e nove foram concluídos. E então veio o que talvez tenha sido o momento mais importante. Erik Panzer decifrou a chamada fórmula recursiva, que gera cada última linha do triângulo a partir da linha acima dela, e que assim nos permite extrapolar do conhecido para o desconhecido.
p
O que passou pela sua cabeça neste momento?
p Uma das coisas que pensei foi, "Ninguém pode ter essa sorte." Percebi que resolveríamos a equação. Na nossa refeição da noite, havia uma garrafa de vinho para nossa mesa ...
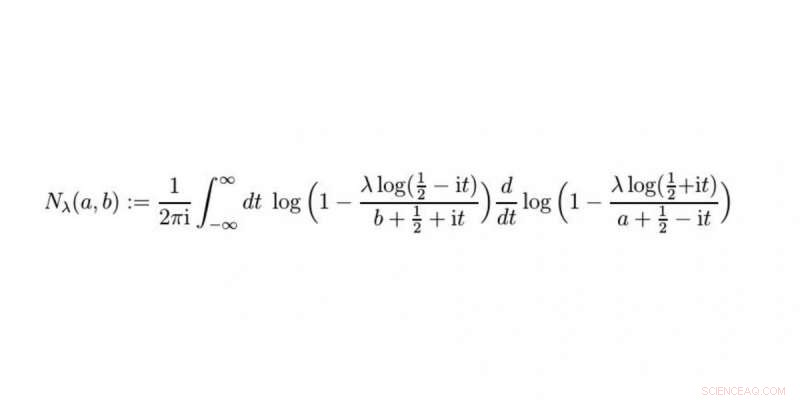 p A função Nielsen faz parte da solução. O Prof. Raimar Wulkenhaar e o Dr. Erik Panzer descobriram esta nova função no decorrer de seu trabalho. Crédito:WWU / Raimar Wulkenhaar
p A função Nielsen faz parte da solução. O Prof. Raimar Wulkenhaar e o Dr. Erik Panzer descobriram esta nova função no decorrer de seu trabalho. Crédito:WWU / Raimar Wulkenhaar
p
… Antes de você voltar ao trabalho.
p sim. No dia seguinte, consegui reduzir parte da equação a uma série simples de derivadas. Inicialmente, o resto parecia difícil. Só tarde da noite tive a ideia de usar a fórmula de Cauchy para resolvê-lo. Ajustei meu despertador para as 5h30 da manhã seguinte e testei imediatamente. Funcionou na primeira tentativa, e na próxima etapa encontrei uma fórmula que costumava ver. Eu sabia que isso seria resolvido usando a função Lambert W. Poucos minutos depois, recebi um e-mail de Erik Panzer:ele também havia pensado na função Lambert, mas por um caminho completamente diferente. Como resultado, alcançamos algo que não era viável há 10 anos:a solução da equação integral que descreve o modelo de uma teoria quântica de campos. Foi simplesmente incrível.
p
Você usa ideias e métodos desenvolvidos por matemáticos no século 18 que foram quase completamente esquecidos hoje em dia.
p Essas fórmulas antigas nos ajudaram muito. A função Lambert W, que é uma parte elementar da nossa solução, tem o nome do matemático suíço Johann Heinrich Lambert. Essa equação surge em um grande número de questões totalmente diferentes. Devido à falta de conhecimento da base de Lambert, a função Lambert foi inventada repetidamente, e só foi estabelecido como padrão em 1993. Também usamos a fórmula de Lagrange-Bürmann, que nos ajudou a resolver uma integral com a ajuda da função de Lambert, bem como a fórmula de Cauchy. Em geral, a matemática tem muito respeito por seus antepassados. Nomes como Euler, Lambert, Lagrange, Cauchy, Gauss e Hilbert são citados com o maior reconhecimento por suas realizações. Mas existem duas ferramentas modernas que eu não gostaria de ficar sem:Wikipedia e álgebra computacional. Você pode encontrar informações abrangentes na Wikipedia cobrindo estruturas e funções matemáticas bem conhecidas - e menos conhecidas. Os computadores podem resolver equações incomparavelmente mais rápido do que manualmente, e sem cometer erros
p
Quais são os próximos passos?
p Uma nova função ocorre em nossa solução, que chamamos de função Nielsen. Quando o entendemos melhor e descobrimos, por exemplo, como ele se relaciona com outras funções conhecidas, submeteremos nosso trabalho - que pode ser acessado gratuitamente on-line como uma pré-impressão - para publicação em uma revista especializada com revisão por pares.
p Depois disso, gostaria de continuar alguns trabalhos em que estou engajado desde 2002 com meu colega Prof. Harald Grosse de Viena. Trata-se de uma teoria quântica de campos para partículas matemáticas. Agora seremos capazes de entender totalmente esse modelo com o auxílio da equação que resolvemos.