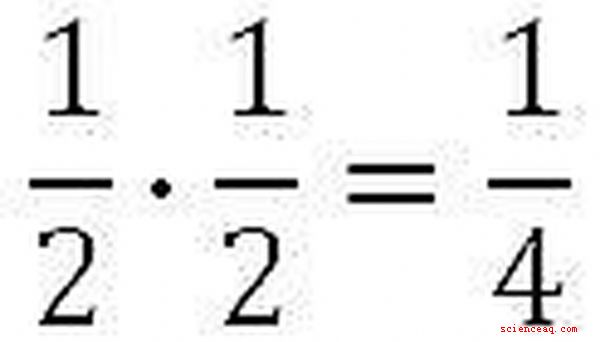
Este é o artigo 1 em uma série de artigos independentes sobre probabilidade básica. Um tópico comum na probabilidade introdutória é resolver problemas envolvendo lançamentos de moedas. Este artigo mostra as etapas para resolver os tipos mais comuns de perguntas básicas sobre esse assunto.

Primeiro, observe que o problema provavelmente fará referência a uma moeda "justa". Tudo isso significa que não estamos lidando com uma moeda "truque", como aquela que foi ponderada para aterrissar em um determinado lado com mais frequência do que teria.

Em segundo lugar, problemas como esse nunca envolvem qualquer tipo de tolice, como a aterrissagem de moeda em sua borda. Às vezes os alunos tentam fazer lobby para ter uma questão considerada nula e sem efeito por causa de algum cenário exagerado. Não leve nada à equação, como a resistência ao vento, ou se a cabeça de Lincoln pesa mais do que a cauda, ​​ou qualquer outra coisa. Estamos lidando com 50/50 aqui. Os professores ficam realmente chateados quando falam de qualquer outra coisa.

Com tudo isso dito, aqui está uma pergunta muito comum: "Uma moeda justa cai na cabeça cinco vezes seguidas. Quais são as chances de que ela caia em cima?" cabeças no próximo flip? " A resposta para a pergunta é simplesmente 1/2 ou 50% ou 0.5. É isso. Qualquer outra resposta está errada.

Pare de pensar sobre o que você está pensando agora. Cada flip de uma moeda é totalmente independente. A moeda não tem memória. A moeda não fica "entediada" de um dado resultado, e deseja mudar para outra coisa, nem tem qualquer desejo de continuar um determinado resultado, já que está "em andamento". Para ter certeza, quanto mais vezes você virar uma moeda, mais perto você chegará a 50% dos flips sendo caras, mas isso ainda não tem nada a ver com qualquer flip individual. Essas idéias compreendem o que é conhecido como a falácia do jogador. Veja a seção de Recursos para mais.

Aqui está outra pergunta comum: "Uma moeda justa é lançada duas vezes. Quais são as chances de que ela caia sobre as duas mãos?" O que estamos lidando aqui são dois eventos independentes, com uma condição "e". Mais simples, cada virada da moeda não tem nada a ver com qualquer outra jogada. Além disso, estamos lidando com uma situação em que precisamos que algo aconteça, "e" outra coisa.

Em situações como as acima, multiplicamos as duas probabilidades independentes juntas. Nesse contexto, a palavra "e" se traduz em multiplicação. Cada flip tem uma chance de 1/2 de aterrissar em heads, então multiplicamos 1/2 vezes 1/2 para obter 1/4. Isso significa que a cada vez que conduzimos esse experimento de duas voltas, temos uma chance de 1/4 de chegarmos a um grande desafio como resultado. Note que nós também poderíamos ter feito este problema com decimais, para obter 0,5 vezes 0,5 = 0,25.

Aqui está o modelo final da questão discutida neste artigo: "Uma moeda justa é lançada 20 vezes seguidas. Quais são as chances de que ele caia na cabeça toda vez? Expresse sua resposta usando um expoente. " Como vimos antes, estamos lidando com uma condição "e" para eventos independentes. Precisamos que o primeiro flip seja heads, e o segundo flip seja heads, e o terceiro, etc.

Devemos calcular 1/2 vezes 1/2 vezes 1/2, repetindo um total de 20 vezes. A maneira mais simples de representar isso é mostrada à esquerda. É (1/2) elevado à 20ª potência. O expoente é aplicado ao numerador e ao denominador. Como 1 ao poder de 20 é apenas 1, poderíamos também escrever nossa resposta como 1 dividido por (2 a 20 de poder).

É interessante notar que as chances reais de acontecer acima são cerca de um em um milhão. Embora seja improvável que qualquer pessoa em particular experimente isso, se você pedir a cada um dos americanos que conduza essa experiência de forma honesta e precisa, um grande número de pessoas relataria sucesso.

Os alunos devem certificar-se de que Estamos à vontade para trabalhar com os conceitos básicos de probabilidade discutidos neste artigo, uma vez que eles surgem com bastante frequência.