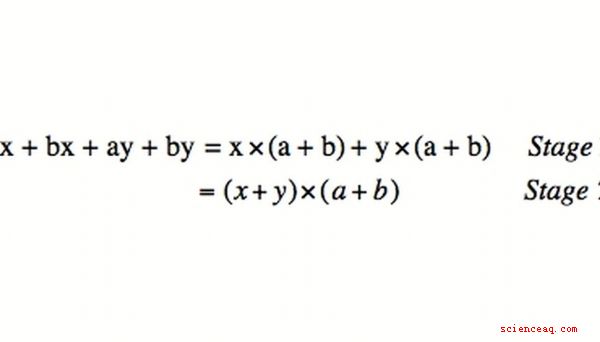
Quadráticos são polinômios de segunda ordem, ou seja, equações de variáveis com expoentes que somam no máximo 2. Por exemplo, x ^ 2 + 3x + 2 é um quadrático. Factoring significa encontrar suas raízes, de modo que (x-root1) (x-root2) seja igual à quadrática original. Ser capaz de fatorar tal fórmula é o mesmo que ser capaz de resolver a equação x ^ 2 + 3x + 2 = 0, já que as raízes são os valores de x onde o polinômio é igual a zero.
Sinais para reverso Método FOIL
O método FOIL reverso para quadrática de factoring faz a pergunta: Como você preenche o formulário (? X +?) (? X +?) Quando fatorando ax ^ 2 + bx + c (a, b, c constantes)? Existem algumas regras para fatoração que podem ajudar a responder isso.
"FOLHA" recebe o nome de seu método de multiplicar fatores. Para multiplicar, digamos, (2x + 3) e (4x + 5), 2 e 4 são chamados de "primeiro", 3 e 5 são chamados de "últimos", 3 e 4 são chamados de "internos" e 2 e 5 são chamados de "internos". "exterior." O formulário poderia, portanto, ser escrito como (FOx + LI) (FIx + LO).
Uma regra de fatoração útil para ax ^ 2 + bx + c é observar que se c > 0, então LI e LO devem ser positivo ou negativo. Da mesma forma, se a é positivo, FO e FI devem ser positivos ou negativos. Se c é negativo, então LI ou LO é negativo, mas não ambos. Novamente, o mesmo vale para a, FO e FI.
Se a, c > 0, mas b < 0, então a fatoração deve ser feita para que LI e LO sejam ambos negativos ou FO e FI ambos negativos. (Não importa qual, pois os dois caminhos levarão a uma fatoração.)
Regras para fatorar quatro termos
Uma regra para fatorar quatro termos de variáveis é extrair termos comuns. Por exemplo, pares em xy-5y + 10-2x têm termos comuns. Puxá-los para fora dá: y (x-5) + 2 (5-x). Observe a semelhança do que está entre parênteses. Portanto, eles podem ser extraídos também: y (x-5) -2 (x-5) se torna (y-2) (x-5). Isso é chamado de "fatoração por agrupamento".
Estendendo Agrupamento a Quadráticos
A regra para fatoração de quatro termos pode ser estendida para quadráticos. A regra para isso é: encontrar fatores de a --- c que somam b. Por exemplo, x ^ 2-10x + 24 tem a --- c = 24 eb = -10. 24 tem 6 e 4 como fatores, que somam 10. Isso nos dá uma dica sobre a resposta final que estamos procurando: -6 e -4 também multiplicam para dar 24, e somam para b = -10. br>
Então agora o quadrático é reescrito com b dividido: x ^ 2-6x-4x + 24. Agora a fórmula pode ser fatorada como ao fatorar por agrupamento, sendo a primeira etapa: x (x-6) + 4 (6-x).