A equação de uma linha é da forma y = mx + b, em que m representa a inclinação e b representa a interseção da linha com o eixo y. Este artigo mostrará, por exemplo, como podemos escrever uma equação para a linha que tem uma determinada inclinação e passa por um dado ponto.

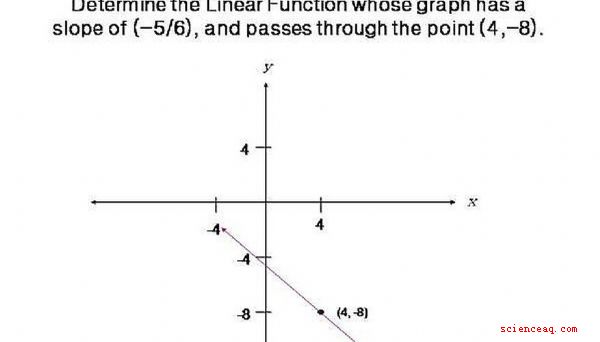
Nós encontraremos a Função Linear cujo gráfico tem uma inclinação de (-5 /6), e passa pelo ponto (4, -8). Por favor, clique na imagem para ver o gráfico.

A fim de encontrar a Função Linear, usaremos o formato Slope-Intercept, que é y = mx + b. M é a inclinação da linha e b é a intercepção y. Nós já temos a inclinação da linha (-5/6), e assim substituiremos m pela inclinação. y = (- 5/6) x + b. Por favor, clique na imagem para uma melhor compreensão.

Agora, podemos substituir x e y com os valores do ponto que a linha passa, (4, -8). Quando substituímos x por 4 e y por -8, obtemos -8 = (- 5/6) (4) + b. Ao simplificar a expressão, obtemos -8 = (- 5/3) (2) + b. Quando multiplicamos (-5/3) por 2, obtemos (-10/3). -8 = (- 10/3) + b. Nós adicionaremos (10/3) a ambos os lados da equação e combinando termos semelhantes, obtemos: -8+ (10/3) = b. Para adicionar -8 e (10/3), precisamos dar -8 um denominador de 3. Para fazer isso, multiplicamos -8 por (3/3), o que equivale a -24/3. Temos agora (-24/3) + (10/3) = b, que é igual a (-14/3) = b. Por favor, clique na imagem para uma melhor compreensão.

Agora que temos o valor para b, podemos escrever a Função Linear. Quando substituímos m com (-5/6) eb com (-14/3) obtemos: y = (- 5/6) x + (- 14/3), que é igual a y = (- 5/6 ) x- (14/3). Por favor, clique na imagem para uma melhor compreensão.