
Crédito CC0:domínio público
Dois pesquisadores da Ohio State University construíram um modelo para explorar ainda mais a oscilação experimentada pela Millennium Bridge em Londres. Em seu artigo publicado na revista Cartas de Biologia , Varun Joshi e Manoj Srinivasan descrevem seu modelo e o que ele mostra.
Em 2000, os engenheiros que projetaram a Millennium Bridge de Londres ficaram surpresos ao descobrir que as multidões de pessoas andando por ela durante uma cerimônia de dedicação a fizeram tremer e balançar - dois dias depois, a ponte foi fechada por razões de segurança. Em estudos subsequentes, os pesquisadores descobriram que a ponte oscilou devido ao comportamento dos pedestres ao caminhar. Quando a ponte se moveu ligeiramente, eles reagiram como alguém parado em um barco a remo tentando evitar que ele virasse. Todas essas pessoas reagindo causaram um loop de feedback que tornou a ponte instável. Neste novo esforço, os pesquisadores aprimoraram os modelos anteriores construídos para imitar o comportamento da ponte e aprenderam mais sobre os movimentos e oscilações.
Os pesquisadores construíram seu modelo pela primeira vez em 2015, com recursos que levavam em consideração coisas como o impacto de indivíduos se movendo em sincronia, mudanças de peso, ou até mesmo ações aleatórias, como pessoas se virando. Mas esse modelo não foi capaz de levar em consideração o custo energético de um indivíduo trabalhando para estabilizar sua marcha. Em seu novo modelo, eles adicionaram a capacidade de levar em consideração o impacto dos ajustes que as pessoas fazem ao caminhar sobre uma superfície instável.
Os pesquisadores descobriram que o balanço da ponte não exigia a sincronia da multidão, que estudos anteriores sugeriram que era necessário para começar a balançar. Eles também descobriram que a sincronização das multidões e a oscilação da ponte não precisavam necessariamente acontecer ao mesmo tempo. O modelo também mostrou que quando a ponte começou a balançar, as pessoas que andam nele alargaram seus passos, que exigia mais energia, mas ofereceu mais estabilidade.
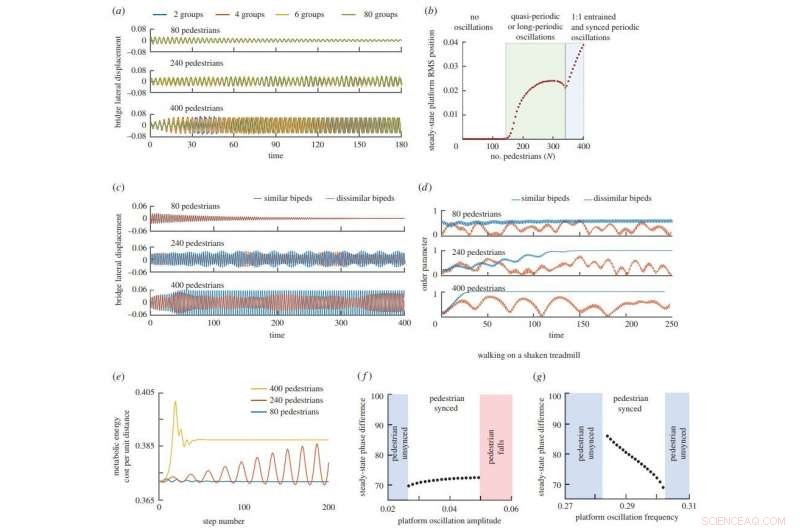
Andando em uma ponte instável. (a) Oscilação da plataforma com P ¼ 2, 4, 6 e 80 grupos de pedestres representando um número equivalente N ¼ 80, 240 ou 400 pedestres. O estado estacionário é independente de P, barramento de time-offsets devido à fase inicial aleatória. Vemos oscilações decadentes para baixo N, oscilações com periodicidade de múltiplas etapas para N intermediário e oscilações periódicas de duas etapas para N grande mostrando três regimes qualitativamente diferentes. (c) Movimento de ponte quando os bípedes (P =8) são idênticos e não idênticos. (d) Variação do parâmetro de ordem mostrando que bípedes idênticos sincronizam, mas bípedes não idênticos não. Veja o material eletrônico suplementar, vídeos para animações de caminhada. (e) O custo de energia para caminhar aumenta quando os pedestres sacodem a ponte, comparando o caso de 400 pedestres (sacudindo) com o caso de 80 pedestres (sem sacudir). Andando em uma esteira abalada. A diferença de fase em regime permanente como uma função de (f) amplitude de oscilação da plataforma e (g) frequência de oscilação da plataforma. Os pedestres entram nas oscilações da plataforma para algumas frequências e amplitudes. Todas as quantidades não dimensionais. Crédito: Cartas de Biologia (2018). DOI:10.1098 / rsbl.2018.0564
Os engenheiros que trabalham no problema de oscilação não tiveram que esperar pelo modelo mais recente para consertá-lo, no entanto, eles instalaram amortecedores que minimizaram drasticamente a oscilação e oscilação, tornando a ponte segura para o tráfego de pedestres.
© 2018 Science X Network