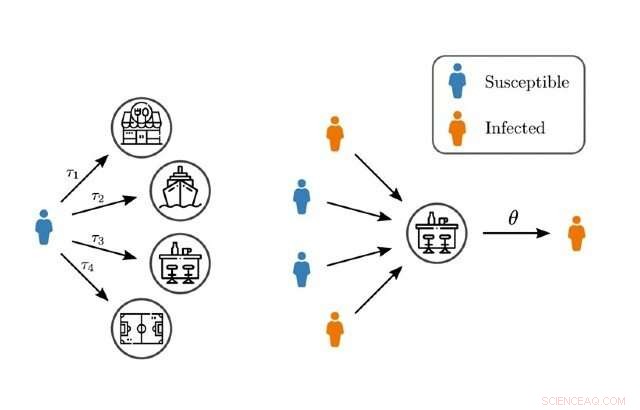
Modelagem de contágios e eventos de superespalhamento por meio de redes de ordem superior. Crédito:Queen Mary, Universidade de londres
Modelos matemáticos têm sido amplamente usados para orientar as decisões do governo sobre a pandemia COVID-19, desde a previsão de resultados até o teste de intervenções potenciais.
Contudo, a complexidade dos cenários do mundo real ainda apresenta novos desafios teóricos para a modelagem matemática da propagação da epidemia.
Por exemplo, evidências de eventos de superespalhamento COVID-19 indicam que é difícil definir as características desses eventos, que pode variar significativamente em sua duração e número de pessoas envolvidas.
Os modelos de rede existentes de propagação da epidemia geralmente se concentram nos contatos entre pares de indivíduos, enquanto a co-localização de indivíduos, como no local de trabalho, restaurantes, ou ginásio normalmente incluem mais de duas pessoas. Eles também muitas vezes deixam de considerar as durações temporais heterogêneas dessas interações em um local específico.
Em um novo estudo, publicado hoje em Cartas de revisão física , os pesquisadores desenvolveram uma nova abordagem para modelagem epidêmica que considera as interações entre duas ou mais pessoas no mesmo local e por diferentes períodos de tempo.
Suposições desafiadoras
O modelo desenvolvido pela equipe de pesquisa internacional, incluindo físicos da Universidade de Vermont e Université Laval, e liderado pela Professora Ginestra Bianconi, um matemático da Queen Mary University of London, também levou em consideração evidências emergentes que sugerem que uma dose infecciosa mínima é necessária para que uma infecção ocorra.
Esta nova abordagem de modelagem muda radicalmente as suposições bem estabelecidas na modelagem de rede epidêmica, como taxas de infecção que são lineares com o número de indivíduos infectados. As descobertas mostram que colocações combinadas com duração heterogênea de exposição podem levar a taxas de infecção não lineares se uma dose infecciosa mínima for necessária para a provável ocorrência de uma infecção.
Professora Ginestra Bianconi, Professor de Matemática Aplicada no Queen Mary, disse:"A co-localização pode envolver grupos de pessoas, enquanto, normalmente, os modelos de rede de propagação da epidemia são baseados em redes de contato que descrevem interações em pares que podem ter uma topologia muito diferente das redes de contato de co-localização. A colocalização também ocorre com o tempo, por exemplo, posso ir para a mesma academia de outra pessoa, mas nem sempre nos encontramos e podemos exercitar por um período diferente de tempo lá. "
"Nossa abordagem abrange as heterogeneidades de interações devido à co-localização que ocorre entre mais de duas pessoas por diferentes períodos de tempo e revela que os núcleos de infecção podem ser não lineares nesses cenários altamente heterogêneos, o que significa que, se houver o dobro de indivíduos infectados visitando um determinado local, a probabilidade de infecção também pode ser duas vezes maior. Esses resultados lançam uma nova luz sobre a natureza muito heterogênea dos eventos de superespalhamento no contexto do COVID-19. "